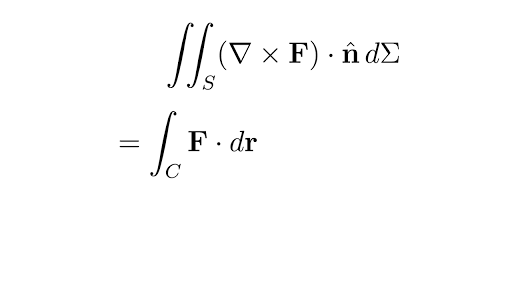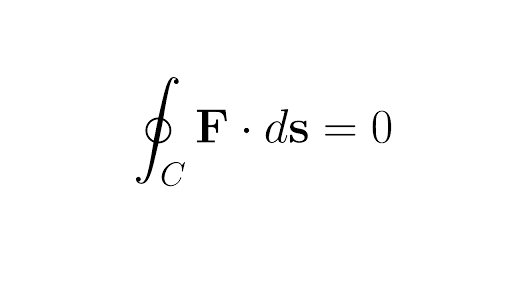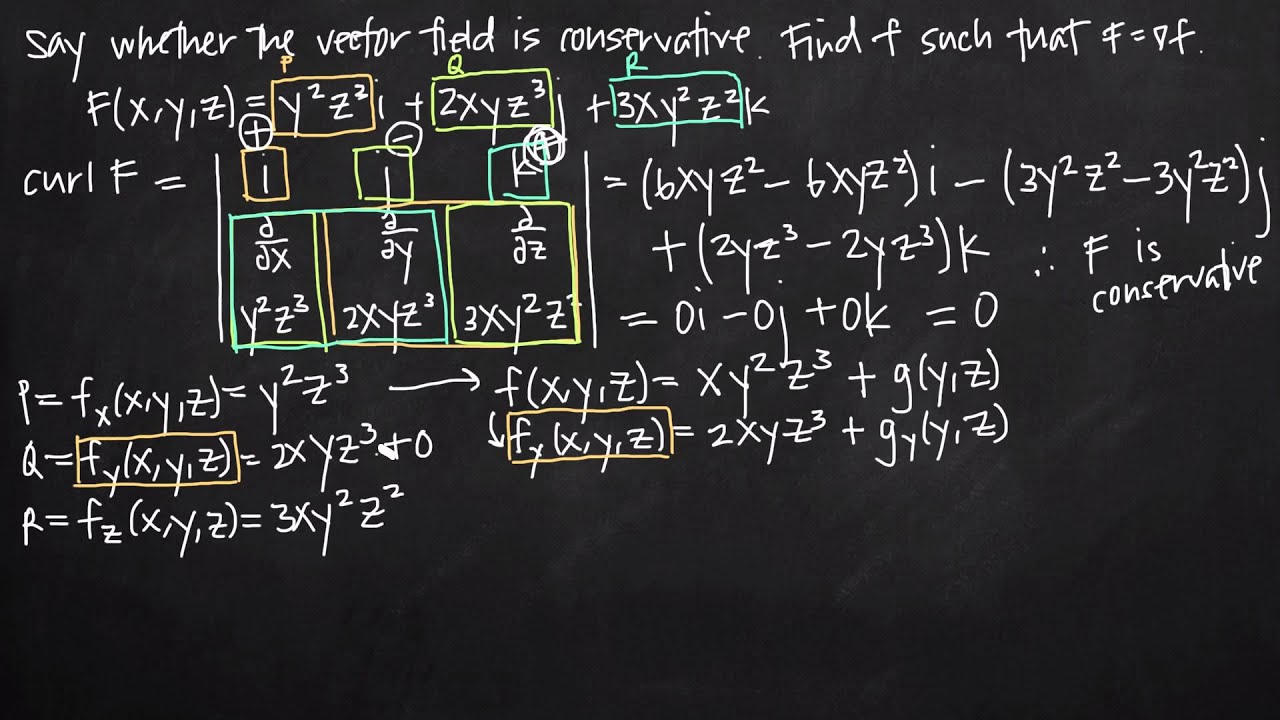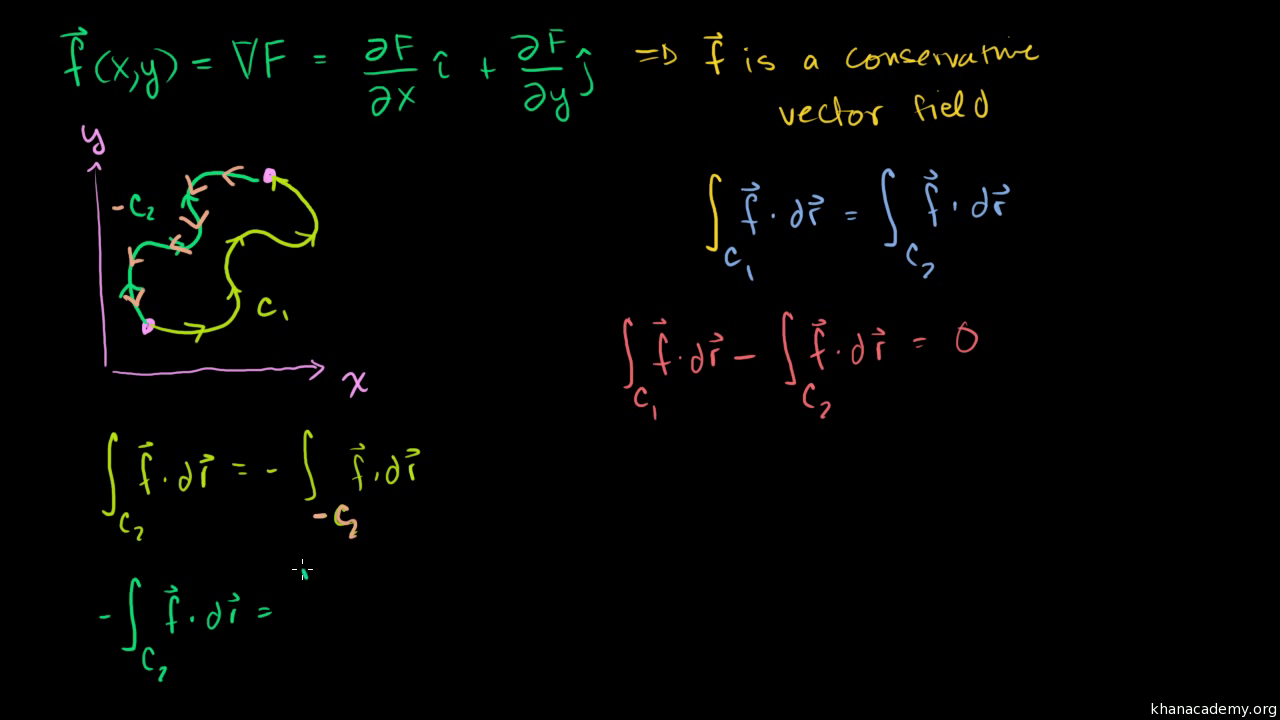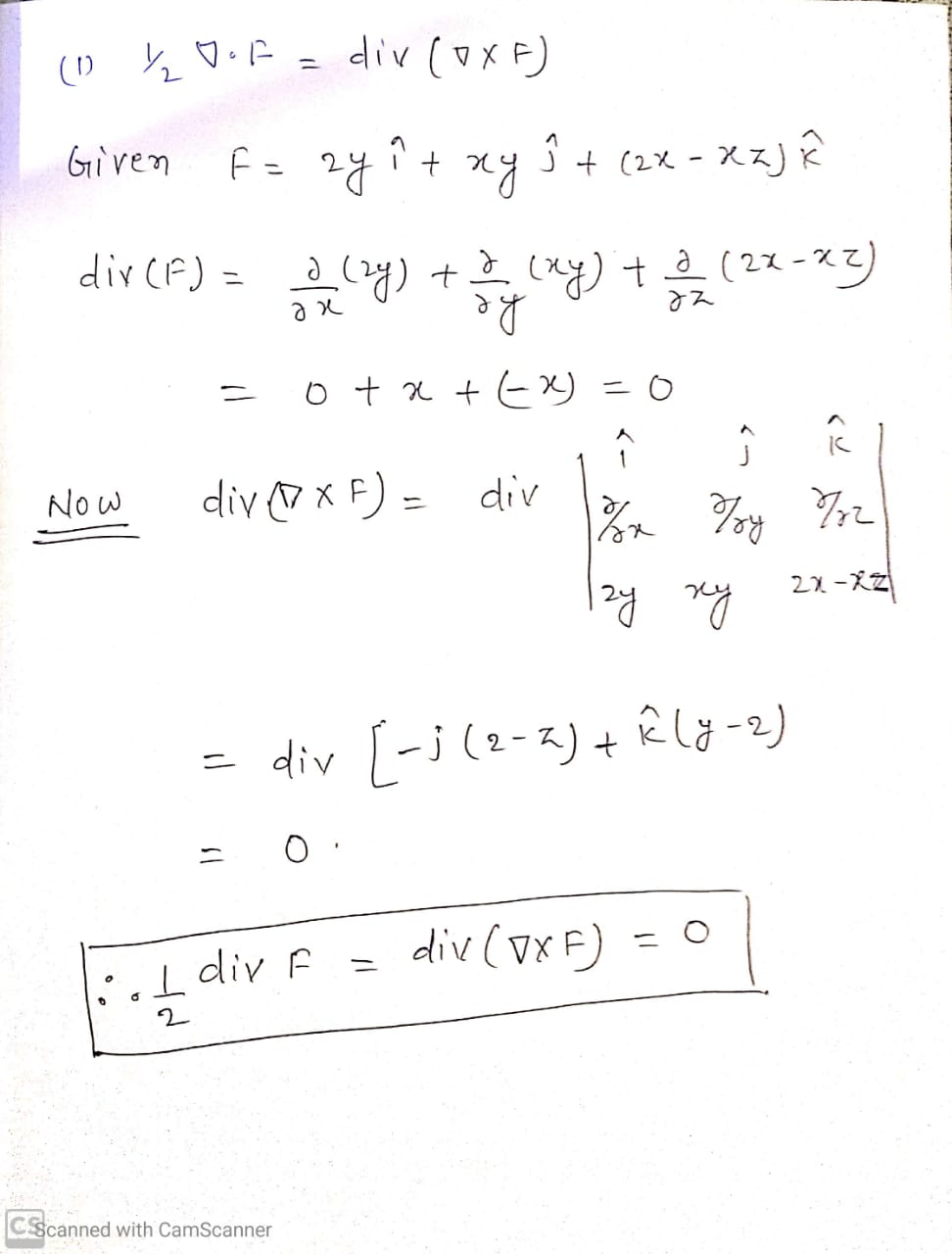Conservative Vector Field 3d

X2siny sqrty2zexpxy logx yz 2.

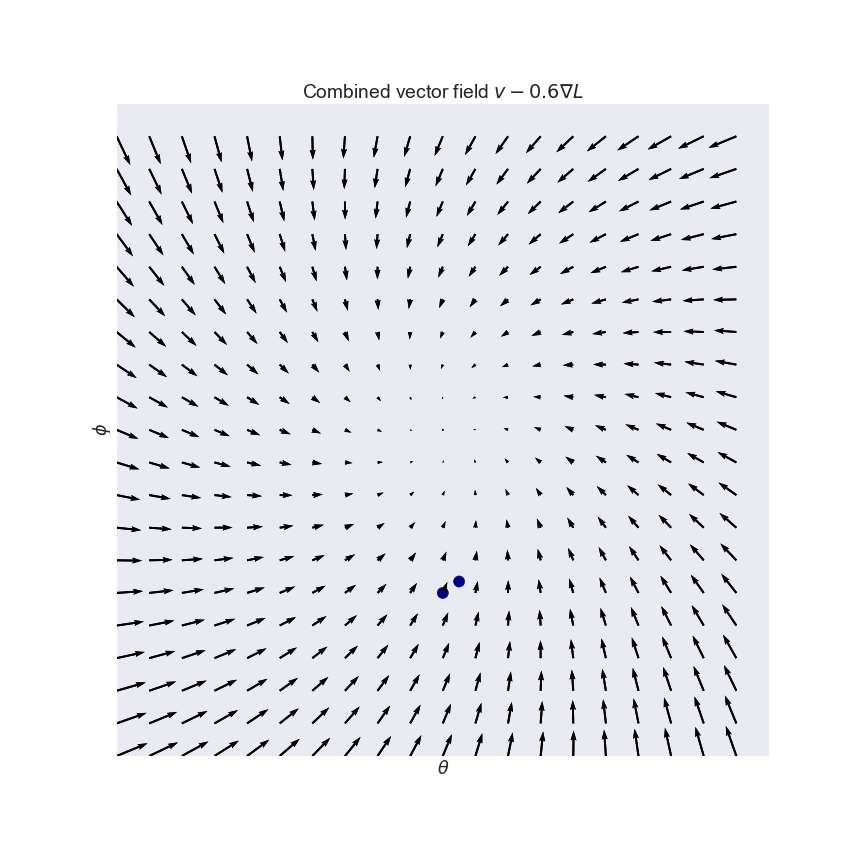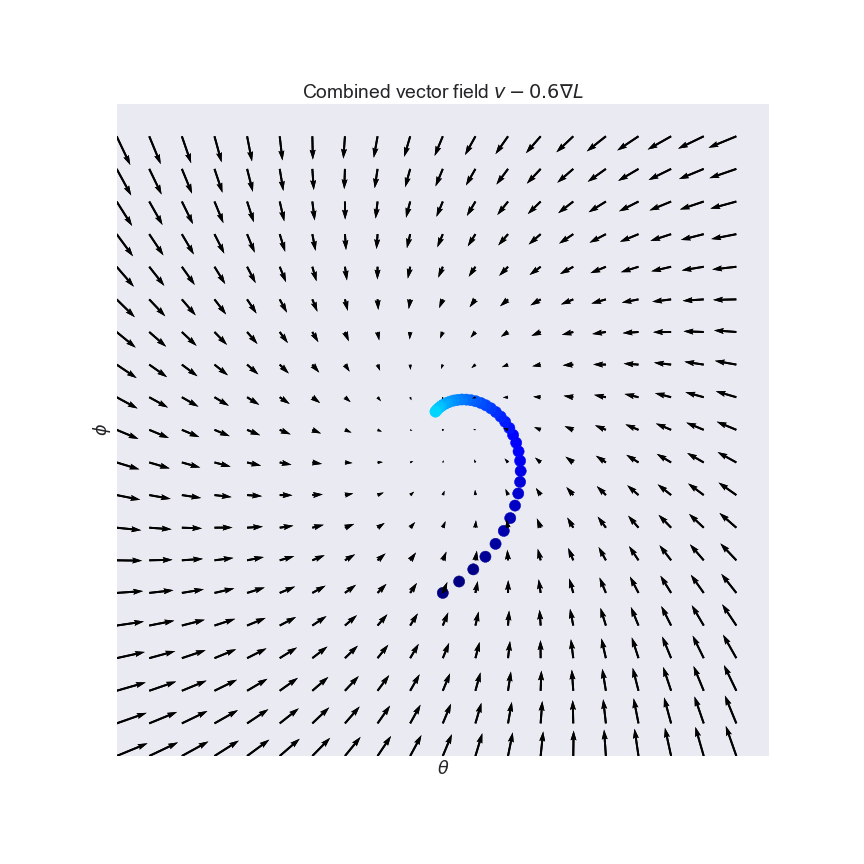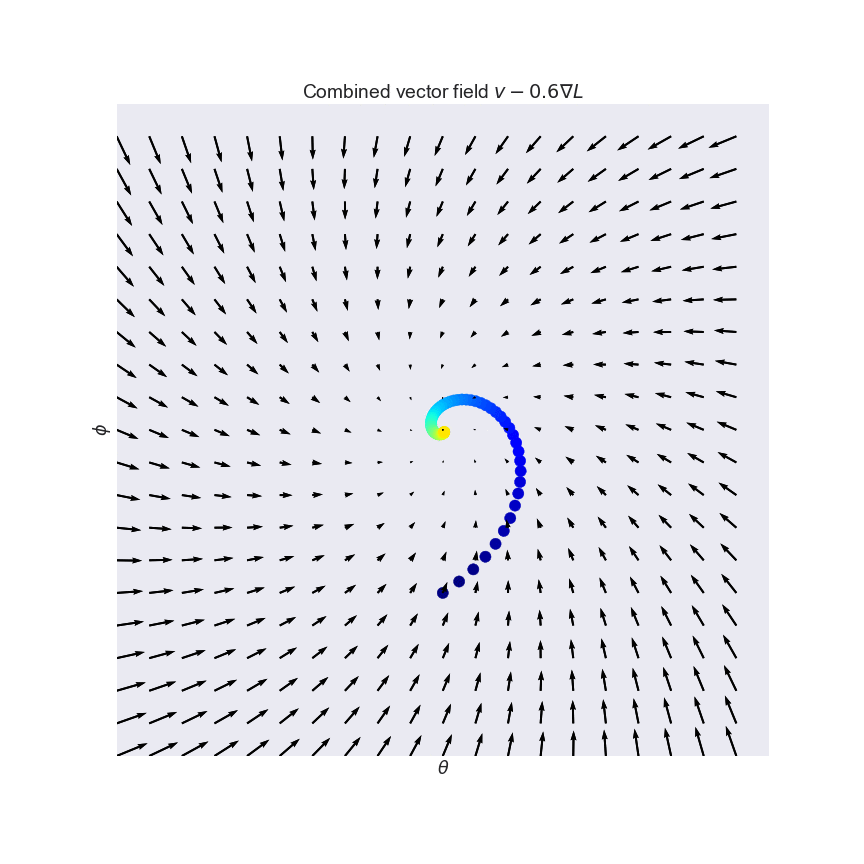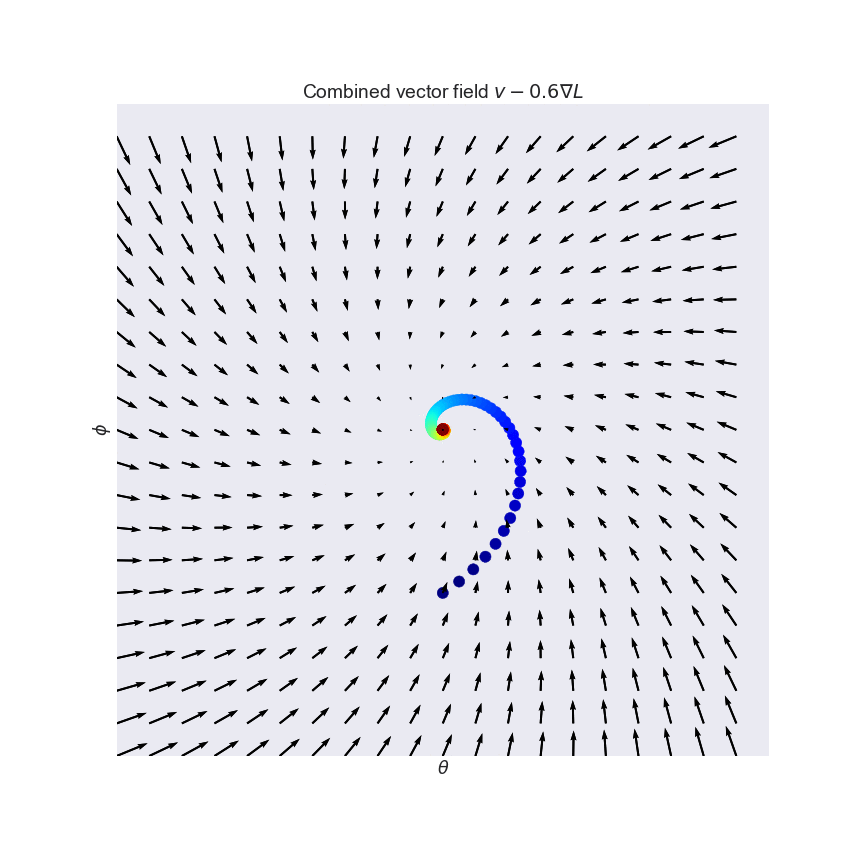
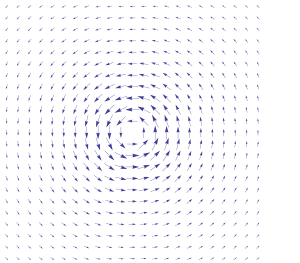
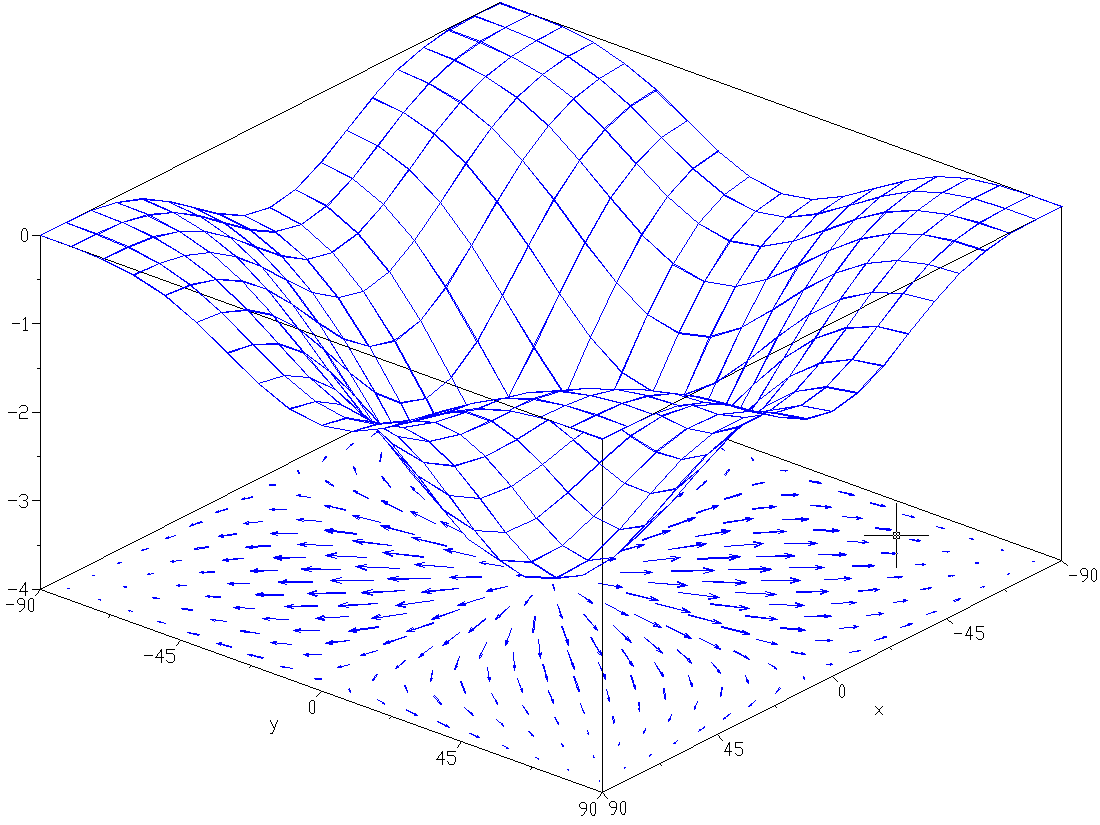
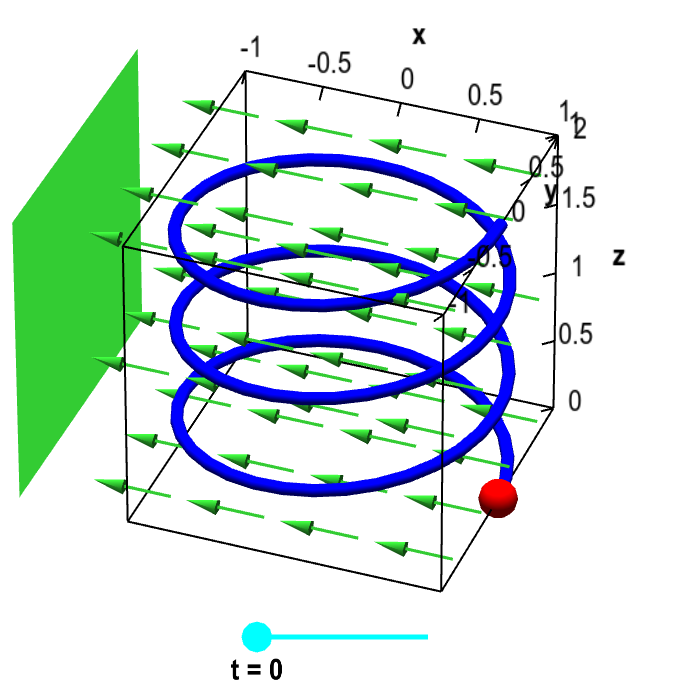
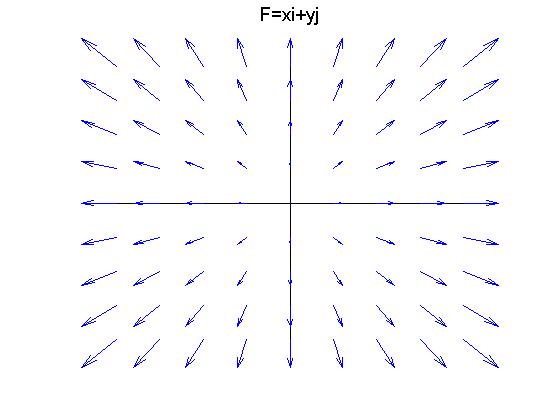
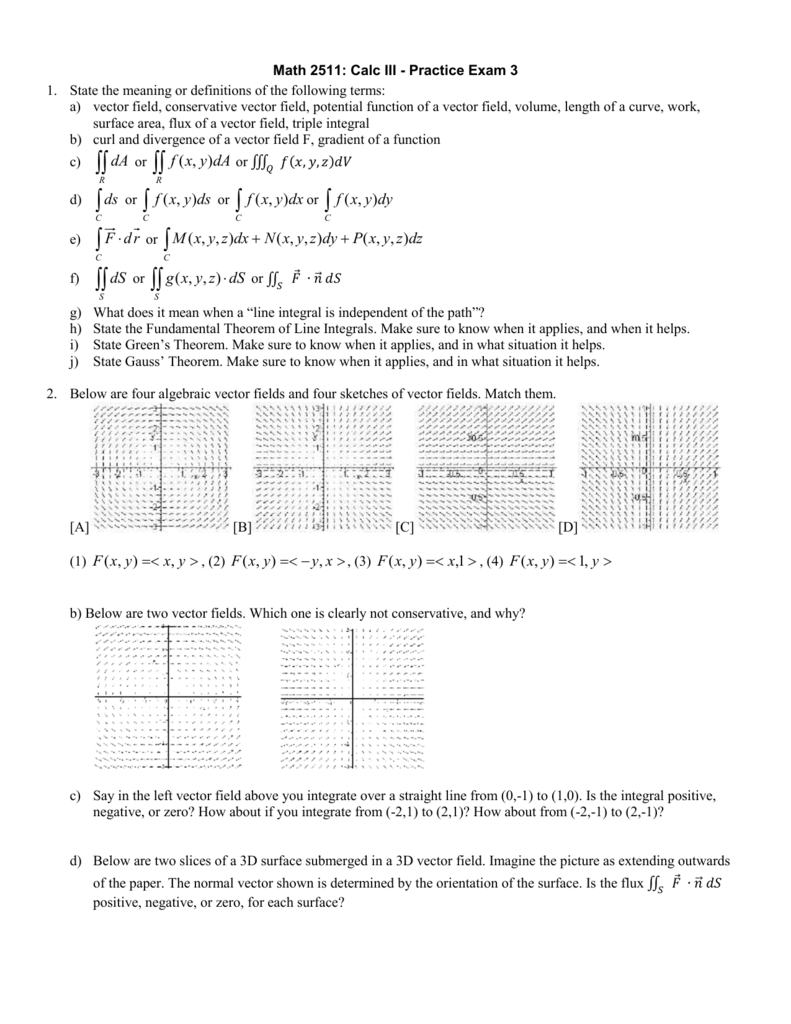
Conservative vector field 3d. F x y textbf f x y fxy start bold text f end bold text left parenthesis x comma y right parenthesis. Path independence of the line integral is equivalent to the vector field being conservative. Conservative fields have the property that their line integral over any path depends only on the end points and is independent of the path travelled. However if we are given that a three dimensional vector field is conservative finding a potential function is similar to the above process although the work will be a little more involved.

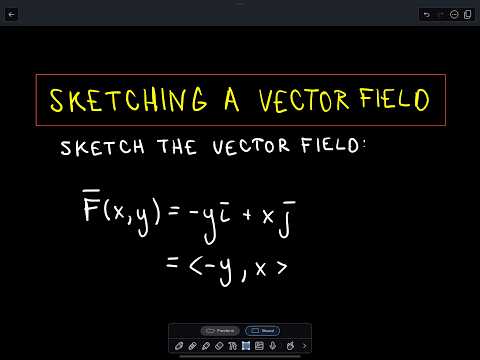
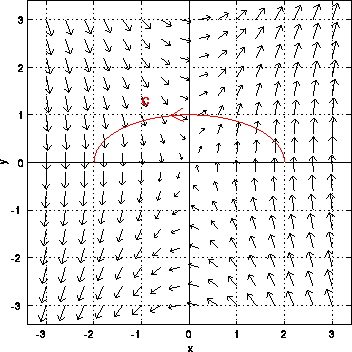
We can show path independence if the curl is zero. F 1 y f 2 x z e y f 1 z f 3 x e y f 2 z f 3 y x e y. By the equality of mixed partials p y f xy f yx q x p z f xz f zx r x q z f yz f zy r y. To visualize what independence of path means imagine three hikers climbing from base camp to the top of a mountain.

Hiker 2 takes a winding route that is not steep from camp to the top. The partial derivatives of f are. A vector field on is a function that assigns to each point a three dimensional vector 1. In three dimensions this means that it has vanishing curl.

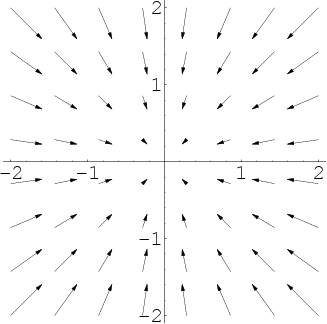
The integral is independent of the path that c takes going from its starting point to its ending point. In vector calculus a conservative vector field is a vector field that is the gradient of some function. Change the components of the vector field by typing for example. A conservative vector field is also said to be irrotational since the.

Hiker 1 takes a steep route directly from camp to the top. Change the scale to provide a better visualisation of the vector field. Is called a conservative vector field if it satisfies any one of the following three properties all of which are defined within the article. Since f is conservative f f for some function f and p f x q f y and r f z.

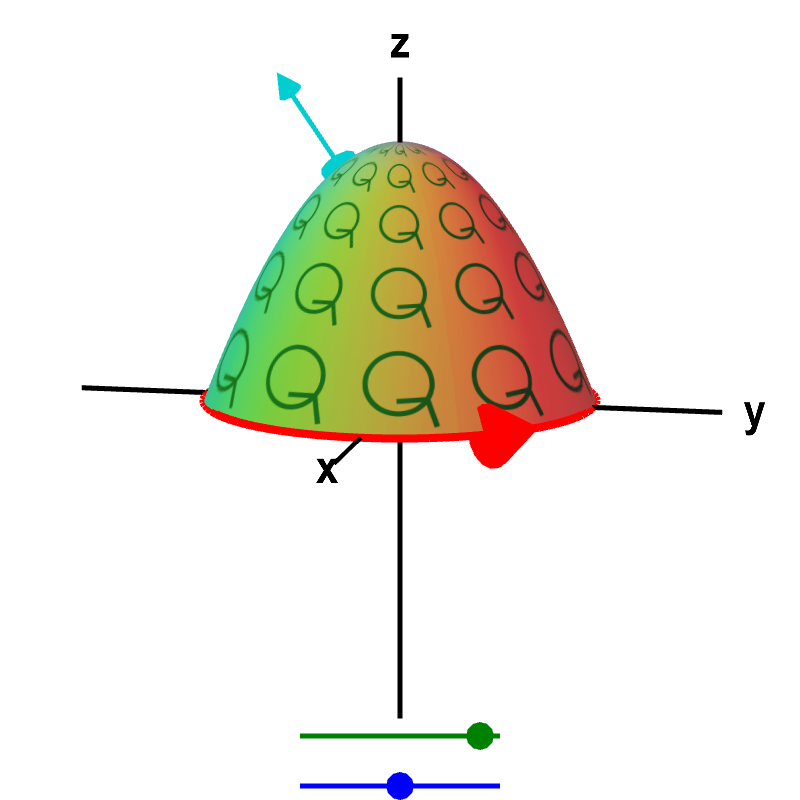
In vector calculus a conservative field is a field that is the gradient of some scalar field. A conservative vector field is also irrotational. The vector field f defined on r 3 which is simply connected. The vector field is conservative and therefore independent of path.

Therefore the curl is zero and f is conservative. If a three dimensional vector field fpqr is conservative then p y q x p z r x and q z r y. Now as noted above we dont have a way yet of determining if a three dimensional vector field is conservative or not. If a three dimensional vector field fpqr is conservative then its curl is identically zero.