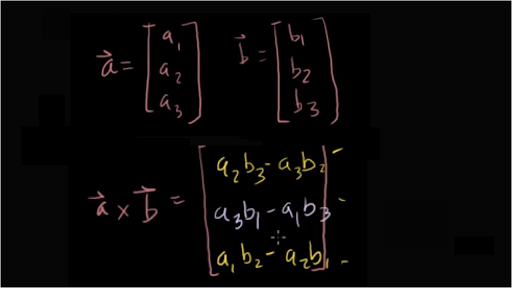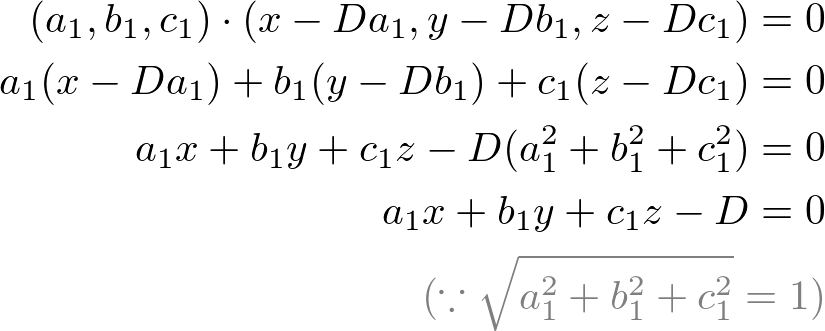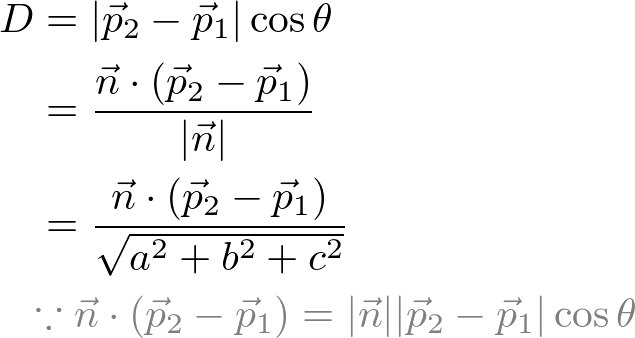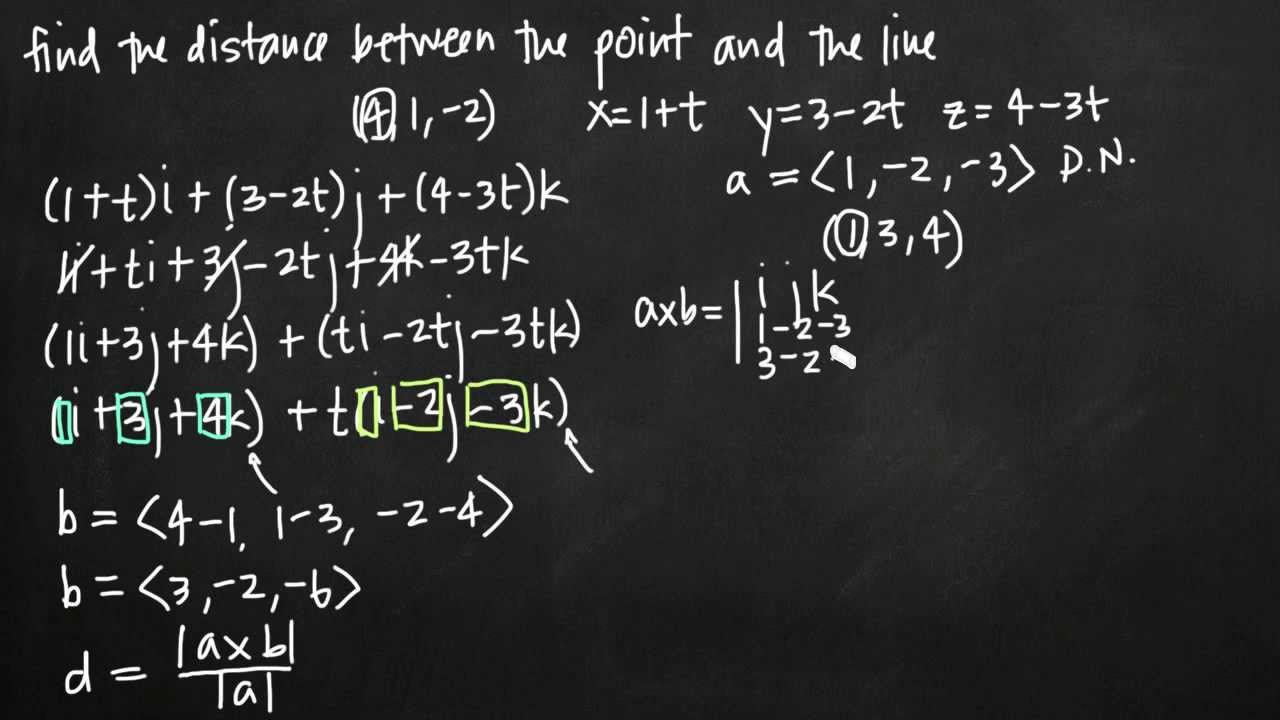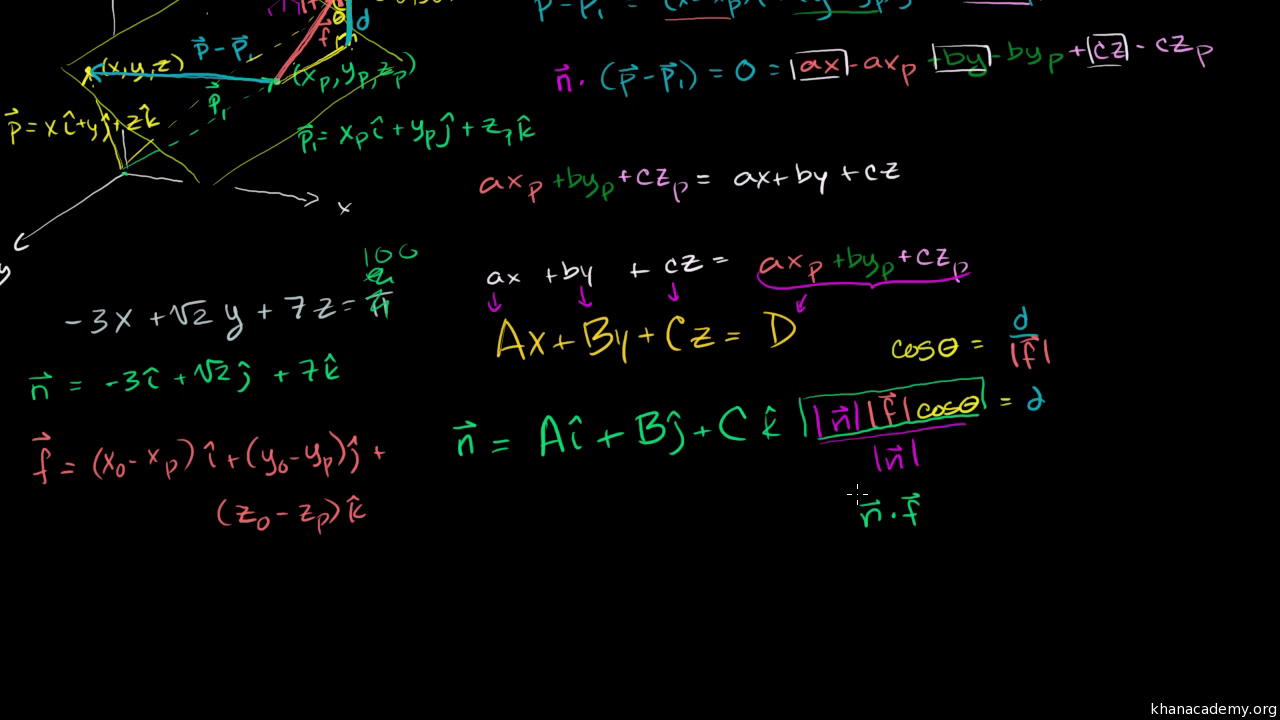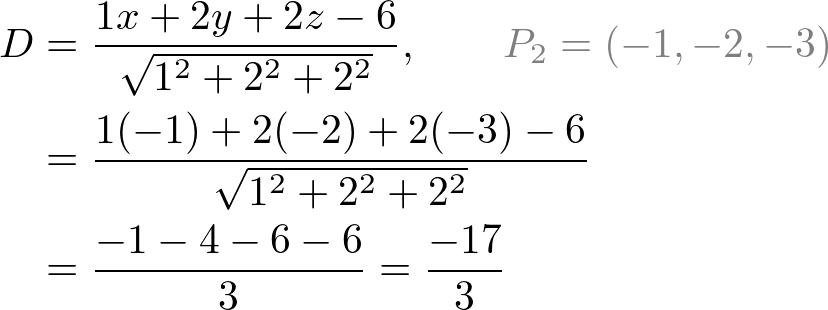Distance Between Point And Line 3d Cross Product

Also let q x 1 y 1 be any point on this line and n the vector a b starting at point qthe vector n is perpendicular to the line and the distance d from point p to the line is equal to the length of the orthogonal projection of on nthe length of this projection is given by. Remember the magnitude of this cross product gives the area of the parallelogram with sides given by the vector ac and ab. The distance of a point to the line is the minimum of all distances from that point to any point on the line.
distance between point and line 3d cross product

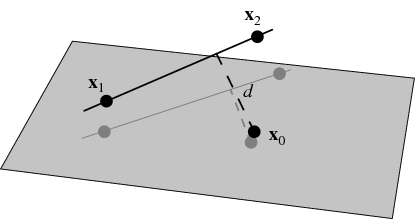
The distance between a point and a line is defined as the shortest distance between a fixed point and any point on the line.

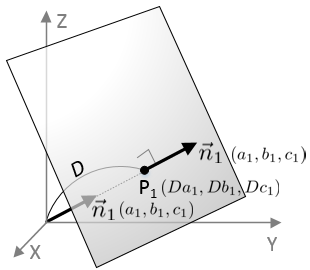
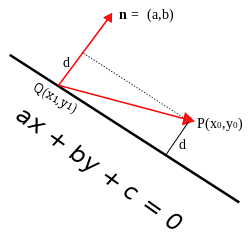
Distance between point and line 3d cross product. Is the distance between p and the plane. Let p be the point with coordinates x 0 y 0 and let the given line have equation ax by c 0. Proof of the formula of distance from a point to a line for the space problem. Basically you find two points on your line.

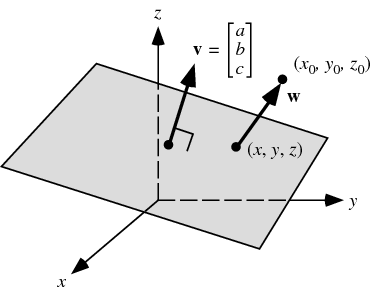
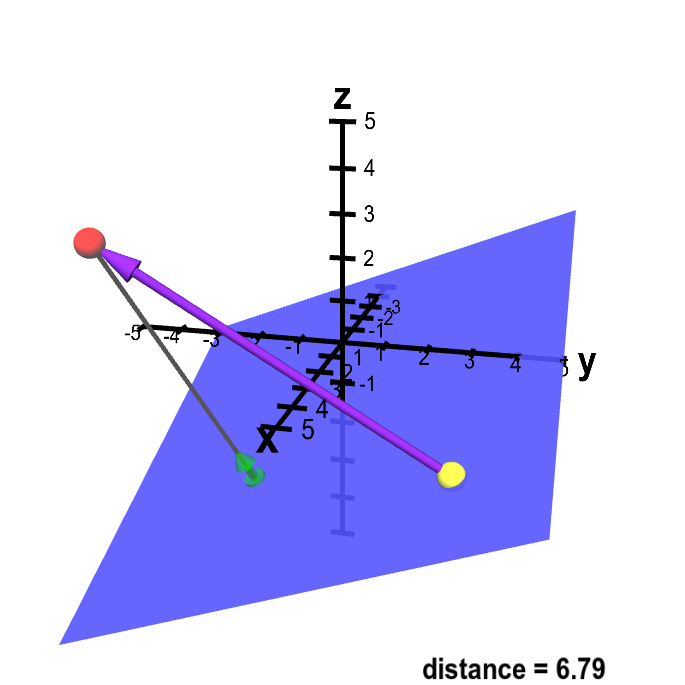
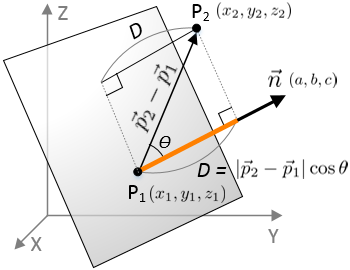
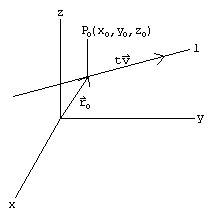
If l is line equation then s m. If p is a point in space and lis the line rt qtu then dpl pq u u is the distance between p and the line l. I want to calculate the shortest distance between p and the line ab. It is the length of the line segment that is perpendicular to the line and passes through the point.

I have a 3d point p and a line segment defined by a and b a is the start point of the line segment b the end. The area divided by base length is height of parallelogram. Calculating the distance of a point to an infinite line was easy as their was a solution on wolfram mathworld and i have implemented that but i need to do this. P is directing vector of line m 1 x 1 y 1 z 1is coordinates of point on line.

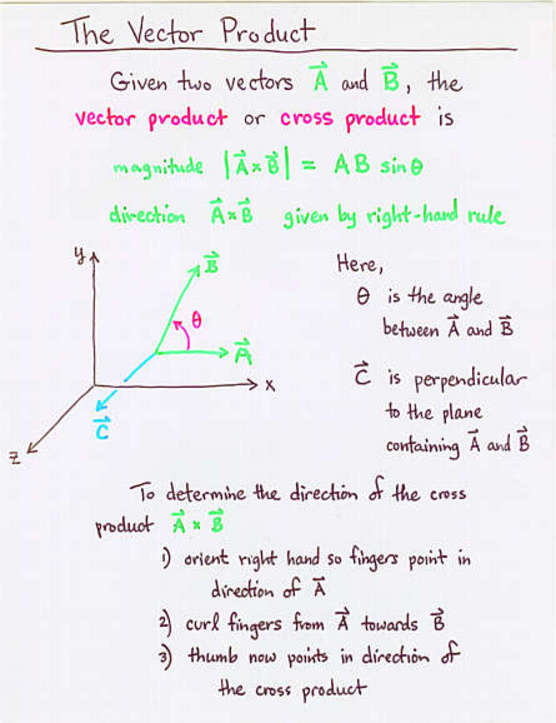
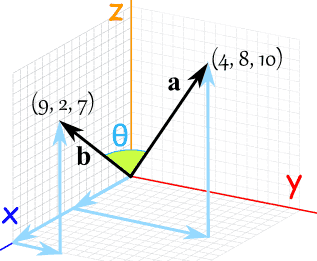
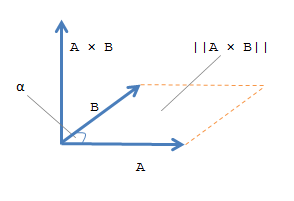
Consider the cross product. From properties of cross product it is known that the module of cross product of vectors is equal to the area of a parallelogramme constructed on. Method 2 using cross product. Explains how to use the cross product of two vectors to find the distance from a point to a line.

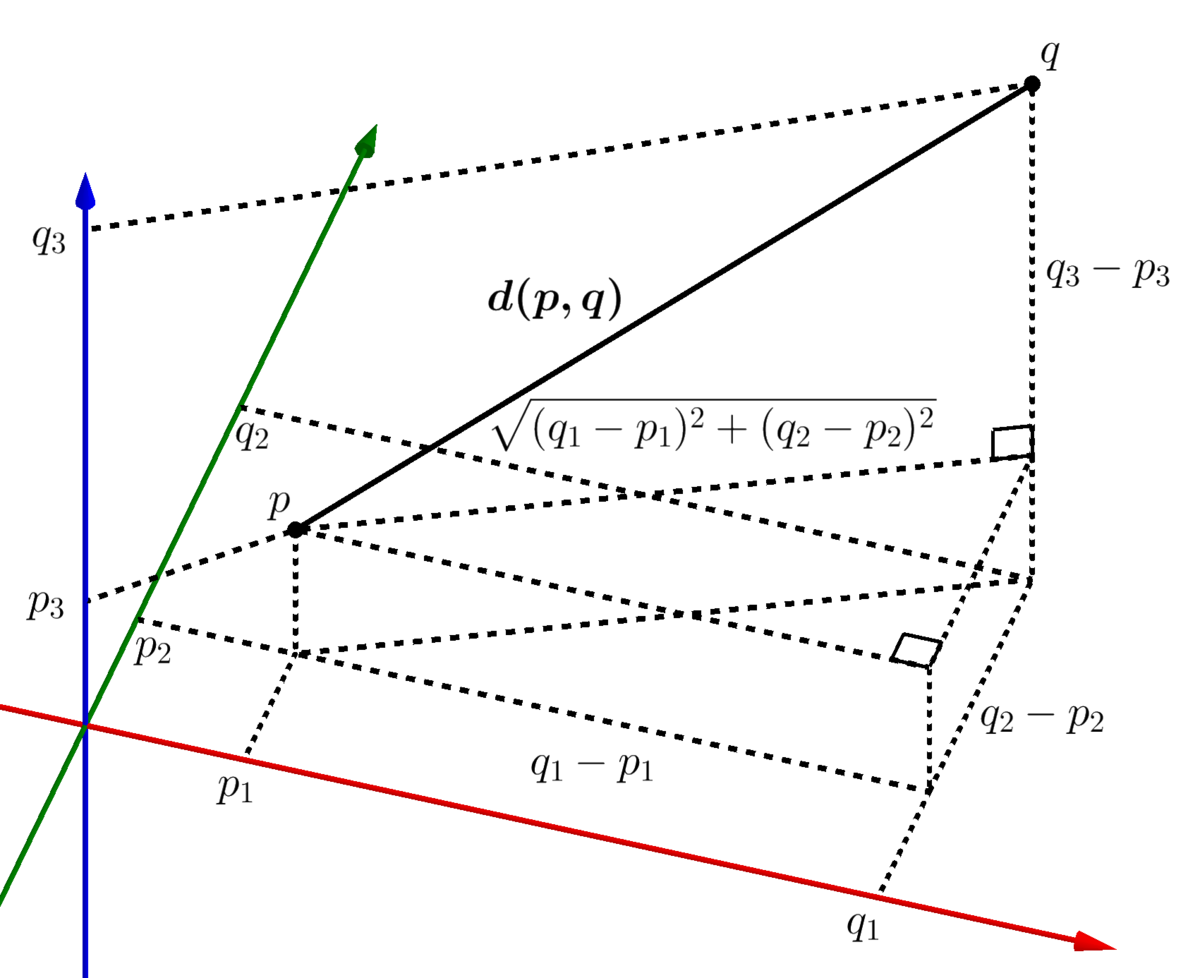
Use the angle formula in the denominator. You have a parametric equation for a line 1 v t v 0 t v 1 to find the minimum distance d between point p and line v t we apply the formula shown in the wolfram mathworld point line distance 3d article noting that in this case x 0 p x 1 v 0 and x 2 v 0 v 1 so x 2 x 1 v 1.