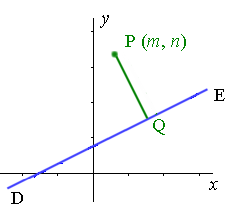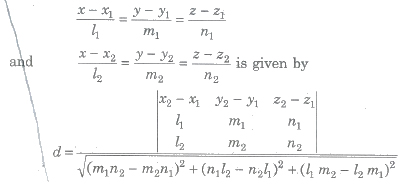Distance Formula In 3d Geometry

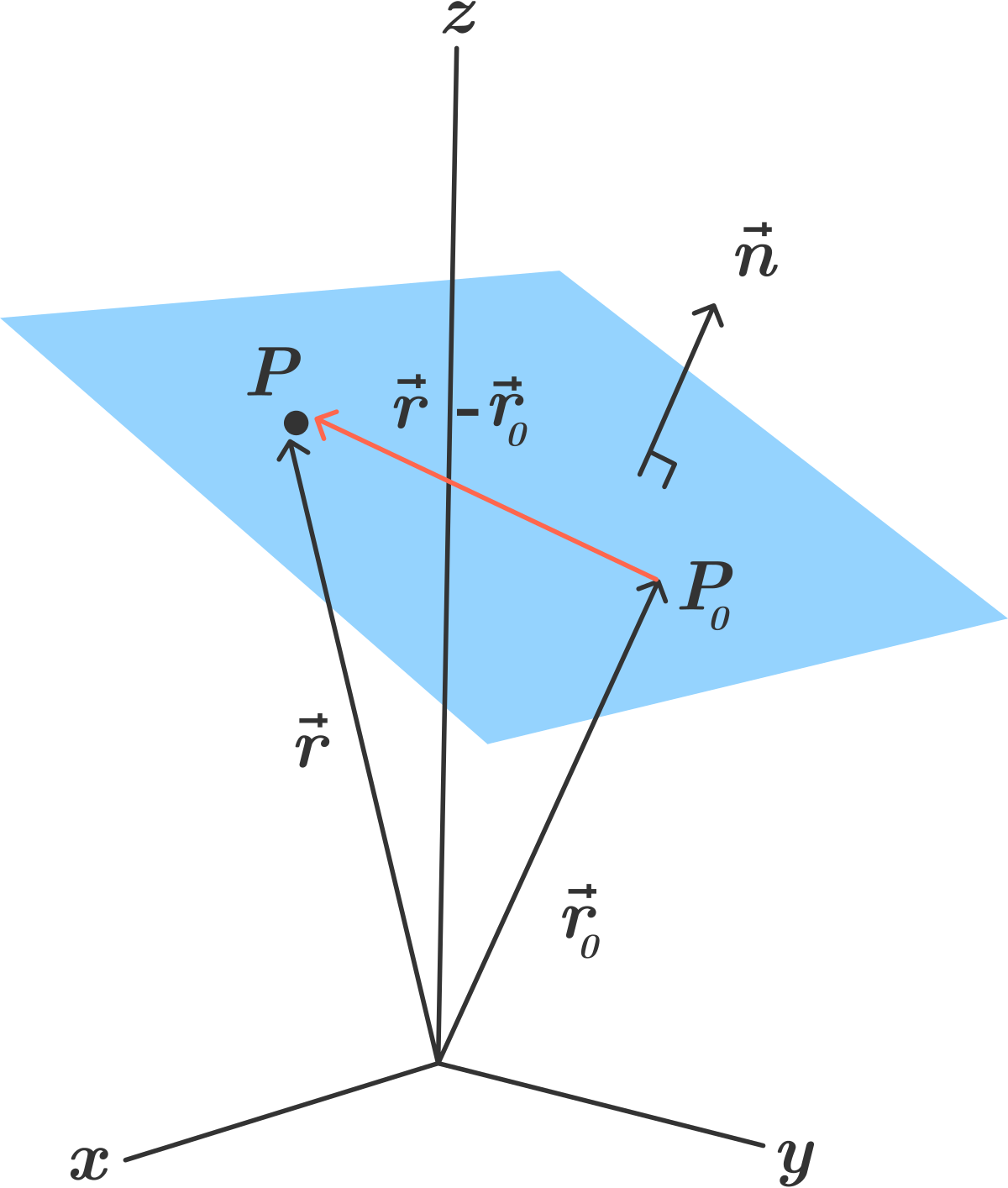
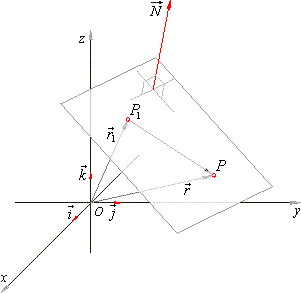
Normal form of a plane.

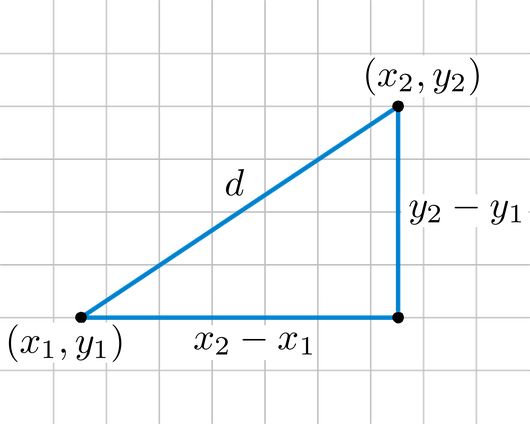
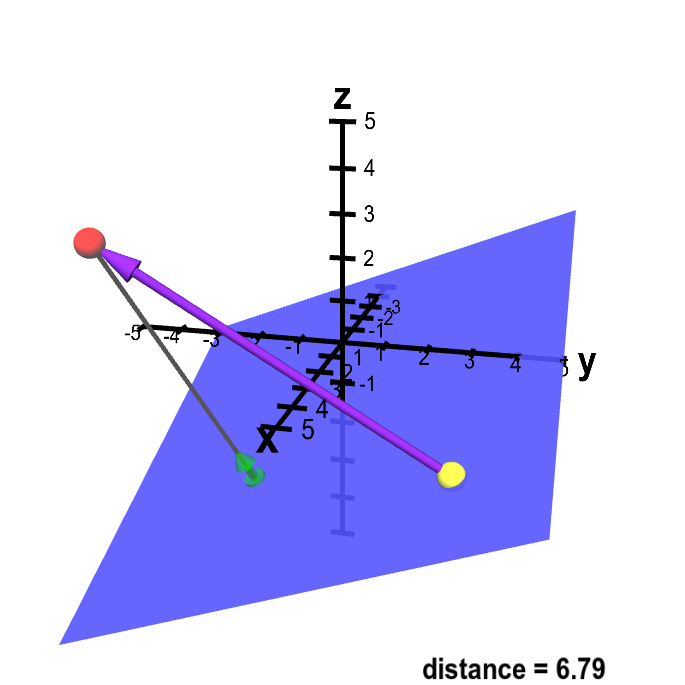
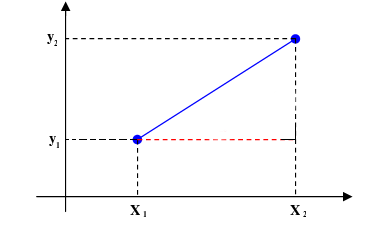
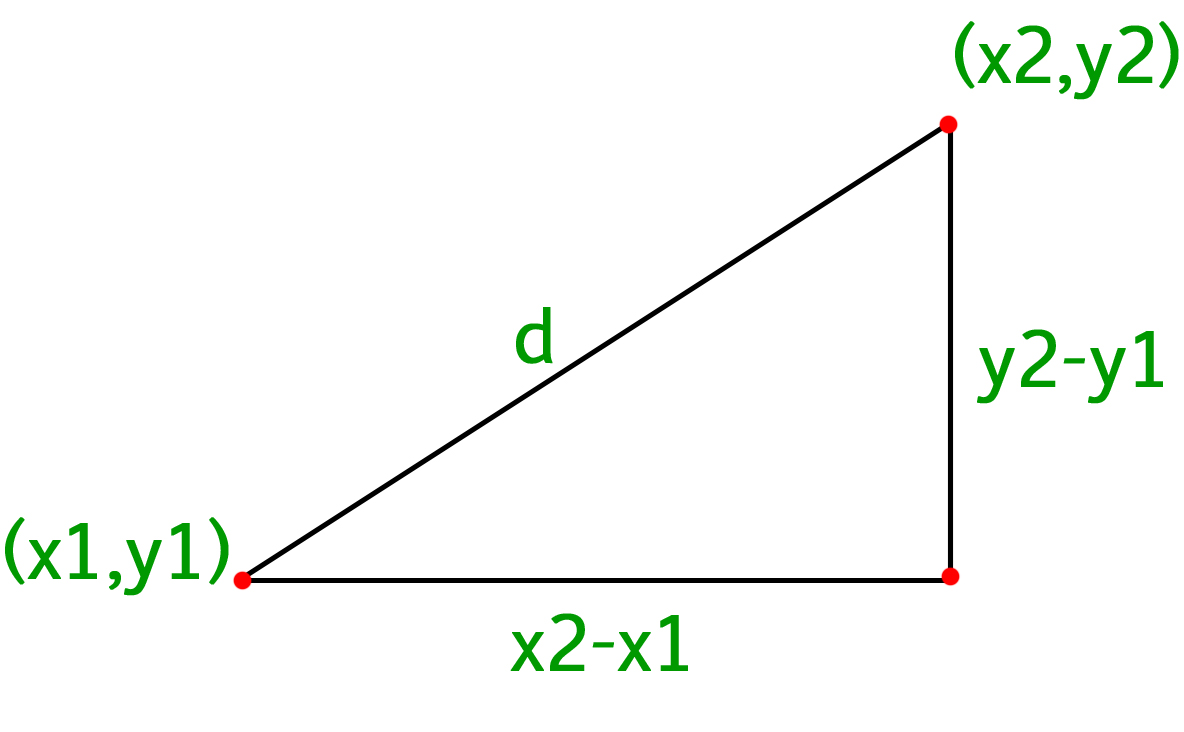
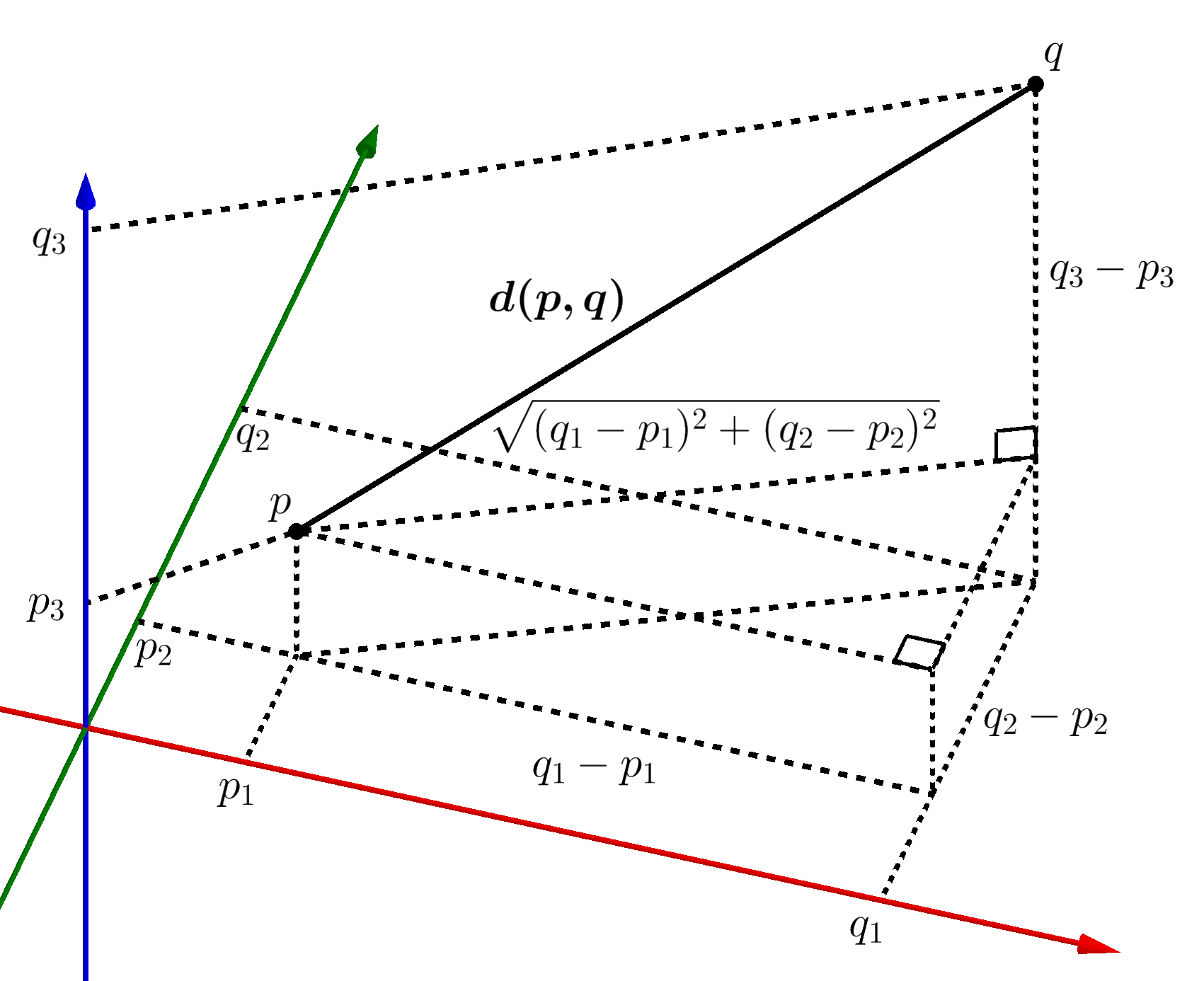
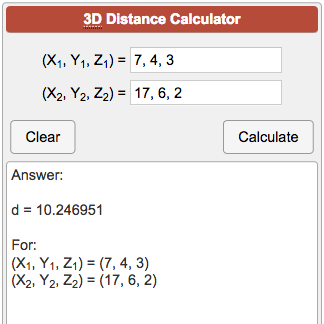
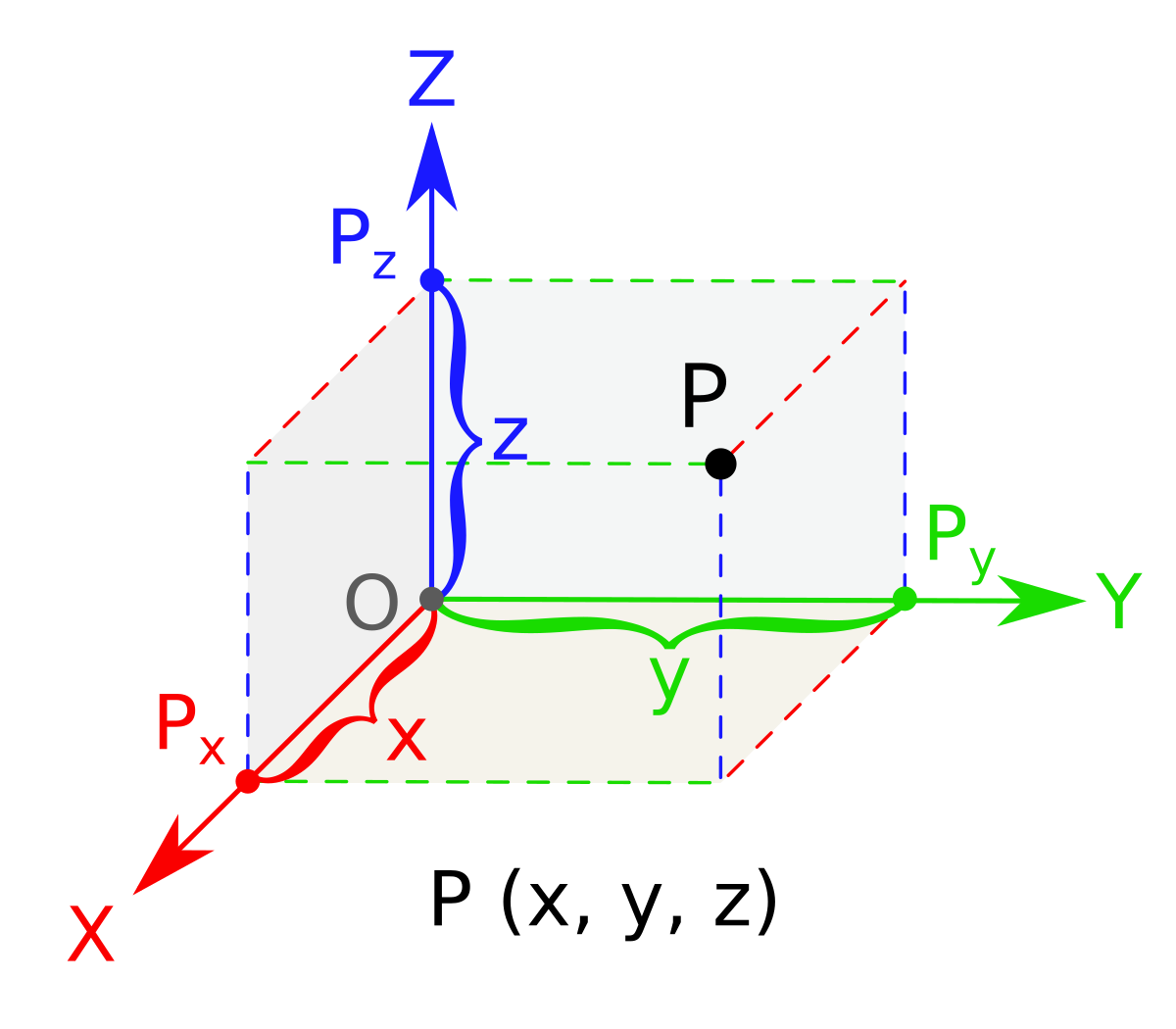
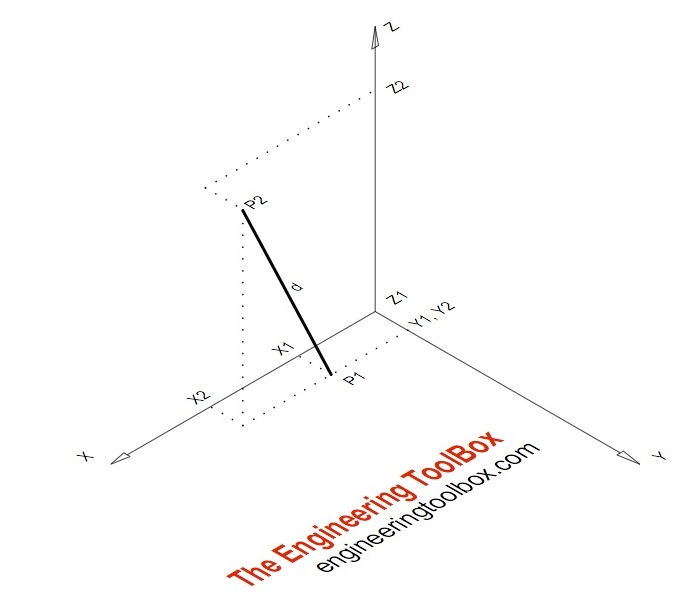
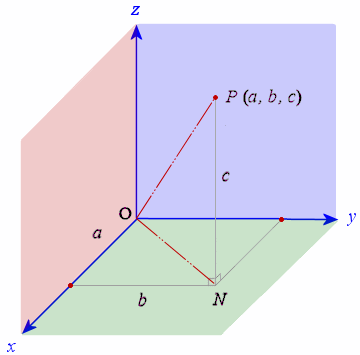
Distance formula in 3d geometry. In a 3 dimensional plane the distance between points x 1 y 1 z 1 and x 2 y 2 z 2 is given by. The distance between two points is the length of the path connecting them. A special case is when the initial point is at the origin which reduces the distance formula to the form dsqrt x 2 y 2 z 2 d x2 y2 z2. The distance formula in 3 dimensions.

Any two straight lines can be differently related to each other in the cartesian plane in the sense that they may be intersecting each other skewed lines or parallel lines. Distance formula and its use in 3d geometry. D x 2 x 1 2 y 2 y 1 2 z 2 z 1 2. Collinearity of three points in 3d.

The above equation is the general form of the distance formula in 3d space. Section formula in 3d. Concept of plane in 3 dimensional geometry. In three dimensional geometry one of the most crucial elements is a straight line.

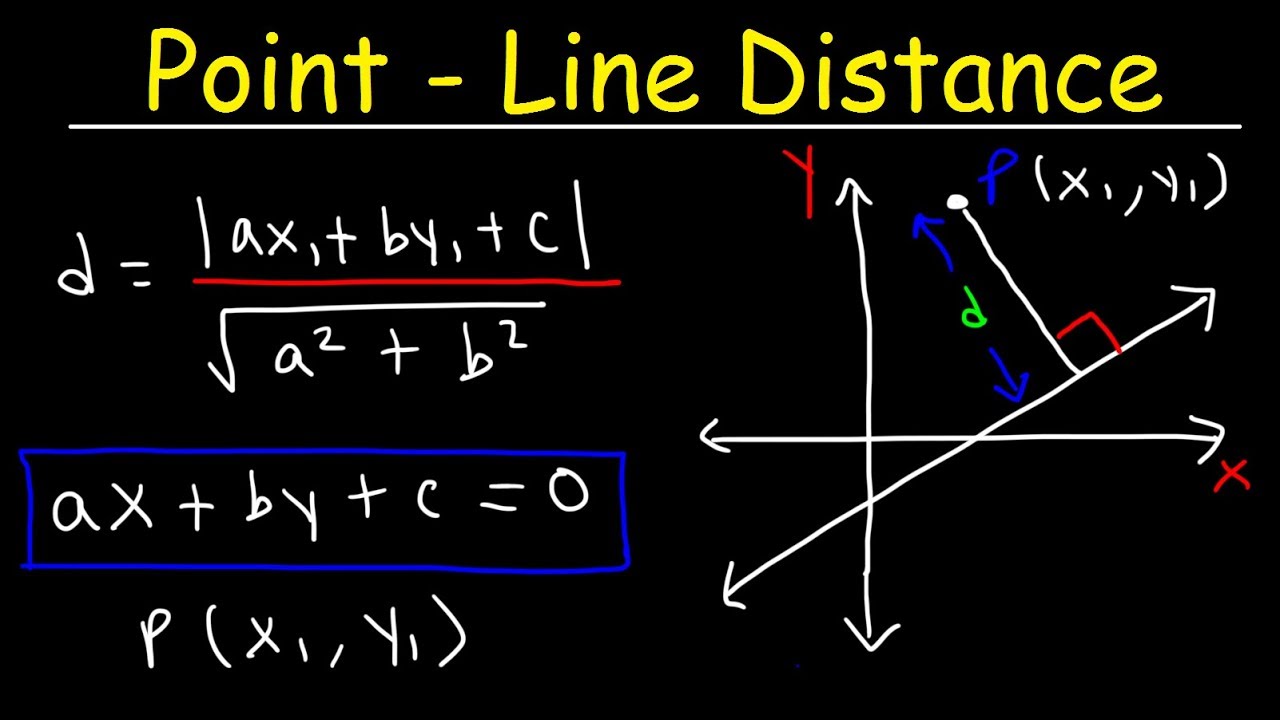
The distance of the point p x 1 y 1 z 1 from the plane is equal to if the plane is given in normal form lx my nz p. Parallel lines in 3d geometry. A first degree equation in x y z represents a plane in 3d. Axbycz0z2b2c20axbycz0z2b2c2ne 0axbycz0z2b2c2 0represents a plane.

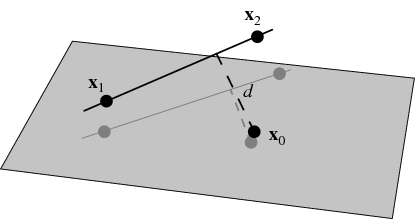
Distance of a point from a plane let the plane in the general form be ax by cz d 0. The shortest path distance is a straight line. Skew lines in 3 d geometry. Distance formula for a 3d coordinate plane.

Other coordinate systems exist but this article only discusses the distance between points in the 2d and 3d coordinate planes. Where x 1 y 1 z 1 and x 2 y 2 z 2 are the 3d coordinates of the two points involved.