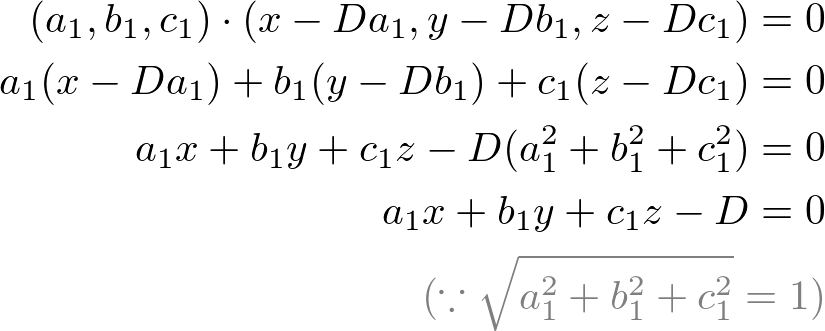Distance Formula In 3d Space
The above equation is the general form of the distance formula in 3d space.
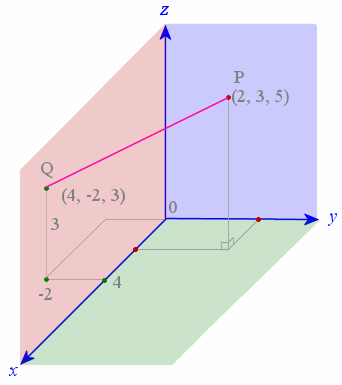
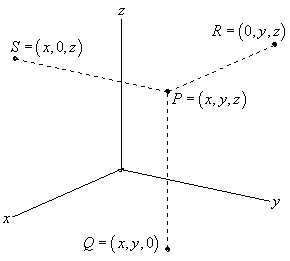
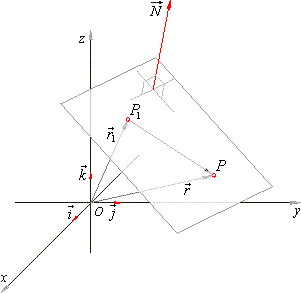
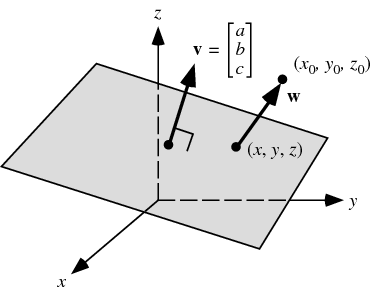
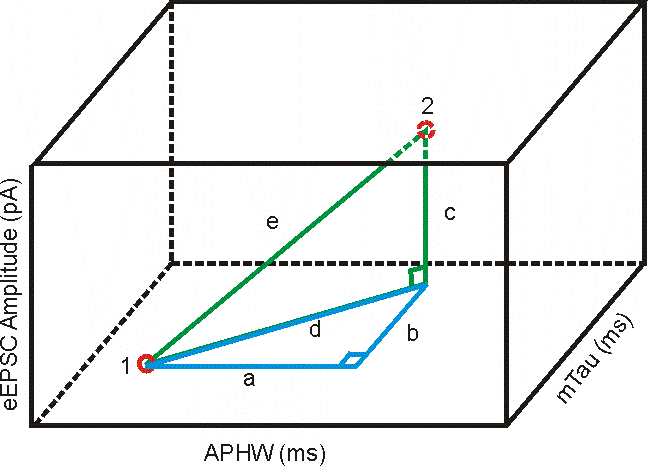
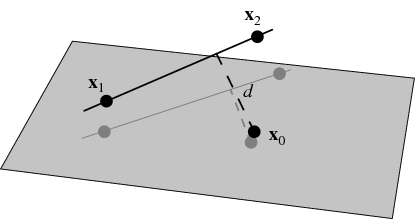
Distance formula in 3d space. Then the shortest distance between the two skew lines will be the projection of pq on the normal which is given by d veca2 veca1. Point a x 0 y 0 z 0. If we have to find the distance between the points in a three dimensional space then we consider here an extra coordinate which is present in the z axis. Distance e would be the distance between cell 1 cell 2.
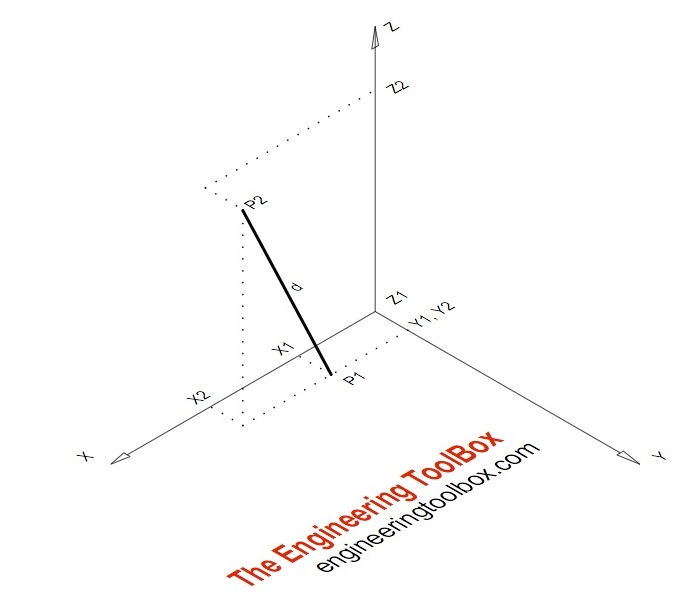
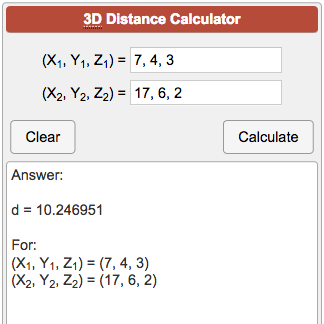
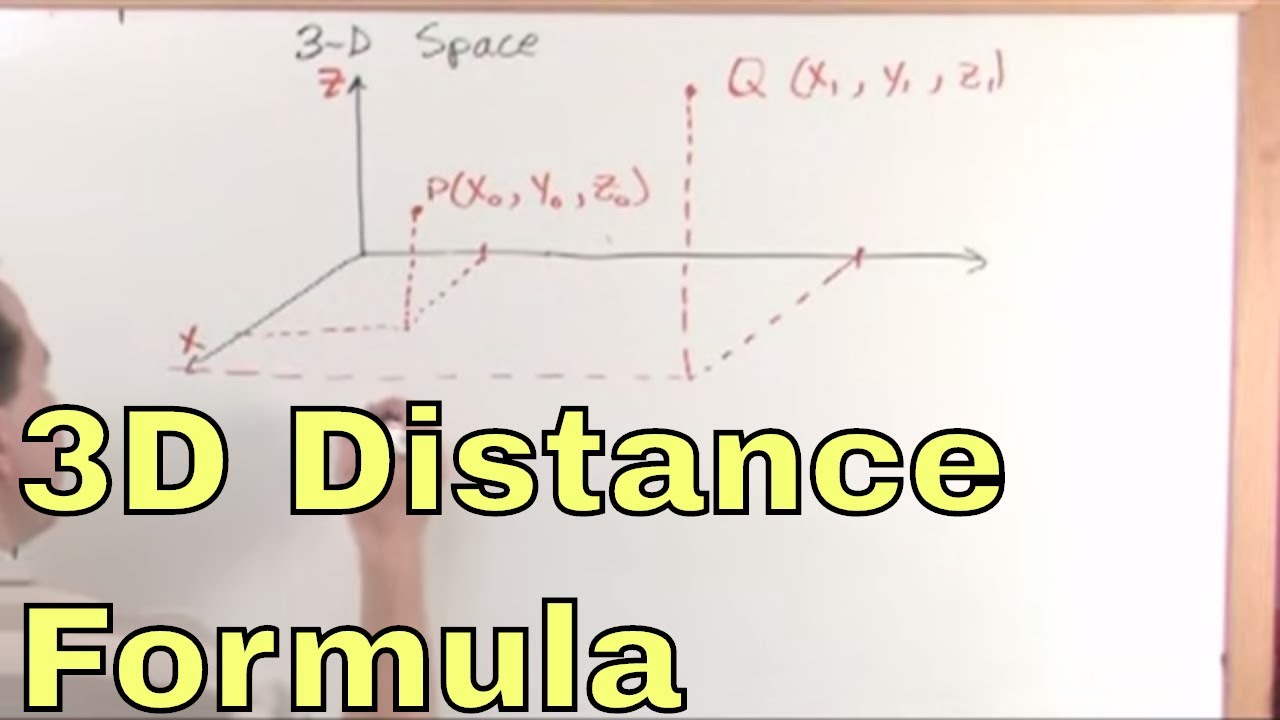
In a 3 dimensional plane the distance between points x 1 y 1 z 1 and x 2 y 2 z 2 is given by. Let us consider two points a x 1 y 1 z 1 and b x 2 y 2 z 2 in 3d space. Y y 0 m y t x x 0 m x t. Thus the formula to find the distance between two points in three dimension is given by.
To remedy this problem we might instead write the line in parametric form. D x 2 y 2 z 2 dsqrt x 2 y 2 z 2 d x 2 y 2 z 2 where x y z xyz x y z is the terminal point. B mtau cell1 mtau cell2. The shortest path distance is a straight line.
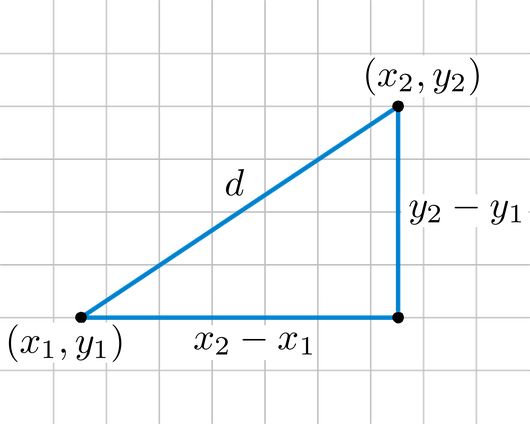
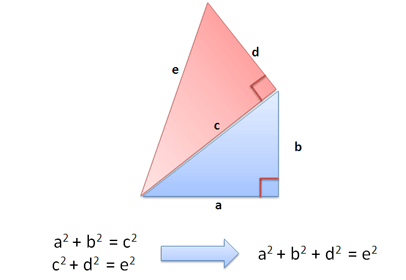
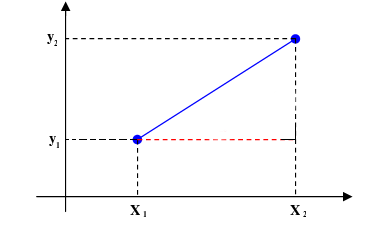
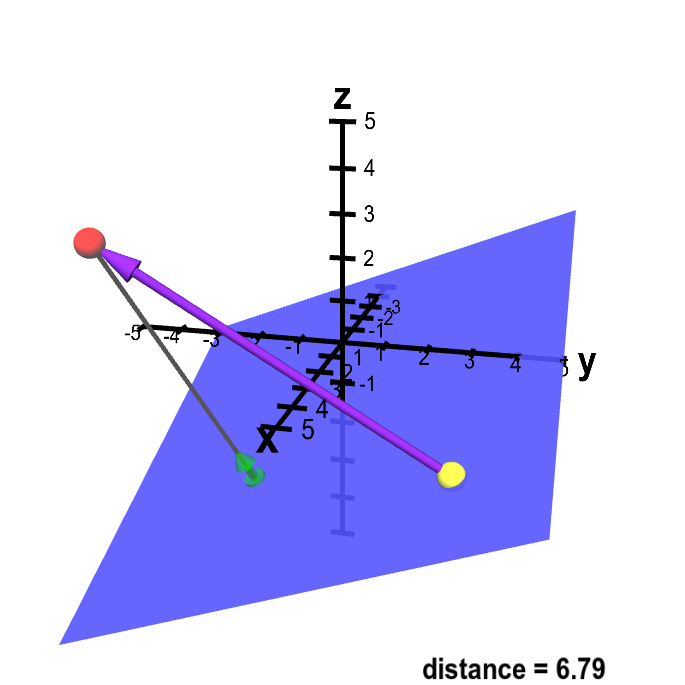
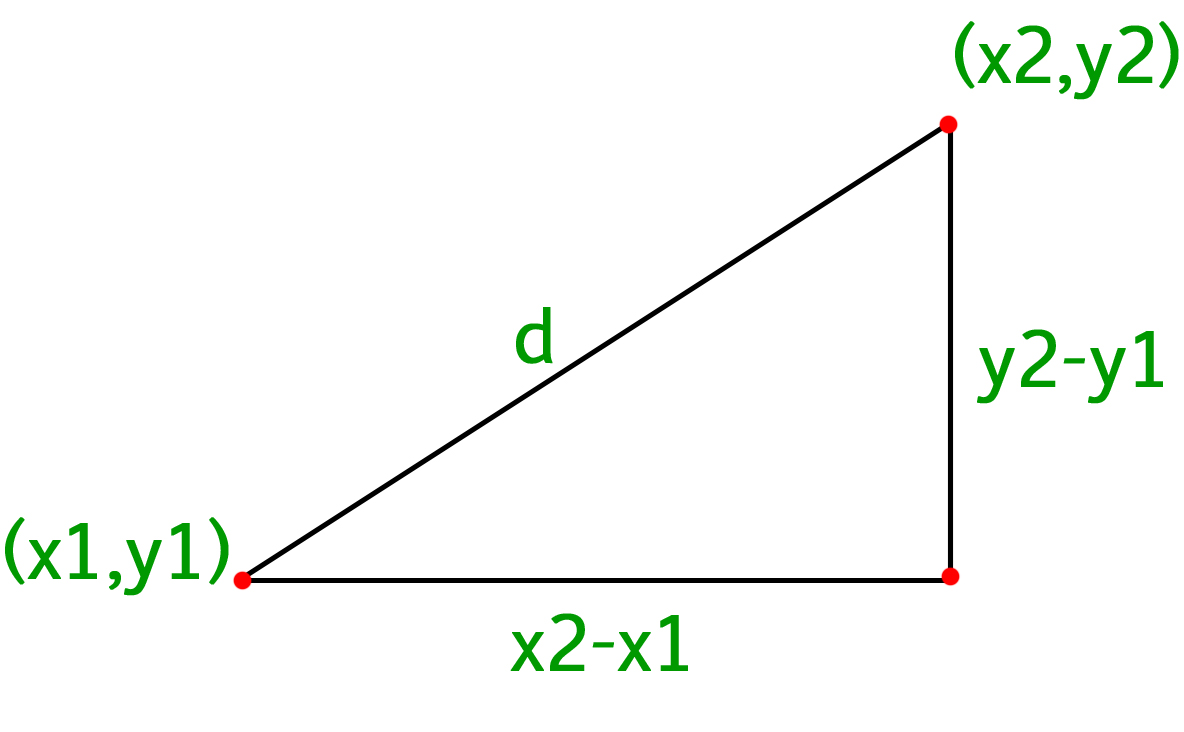
A disadvantage of this formula is that it cannot express lines where x is constant for example the line x 3 this problem arises because we have defined y as a function of x. With 3 variables the distance can be visualized in 3d space such as that seen below. The distance between two points is the length of the path connecting them. A b x 2 x 1 2 y 2 y 1 2.
Pqsqrtx2 x1 2y2 y1 2z2 z1 2 this formula gives us the distance between two points px1y1z1 and qx2y2z2 in three dimensions. Show activity on this post. Point b x 1 y 1 z 1 the distance is in units. A aphw cell1 aphw cell2.
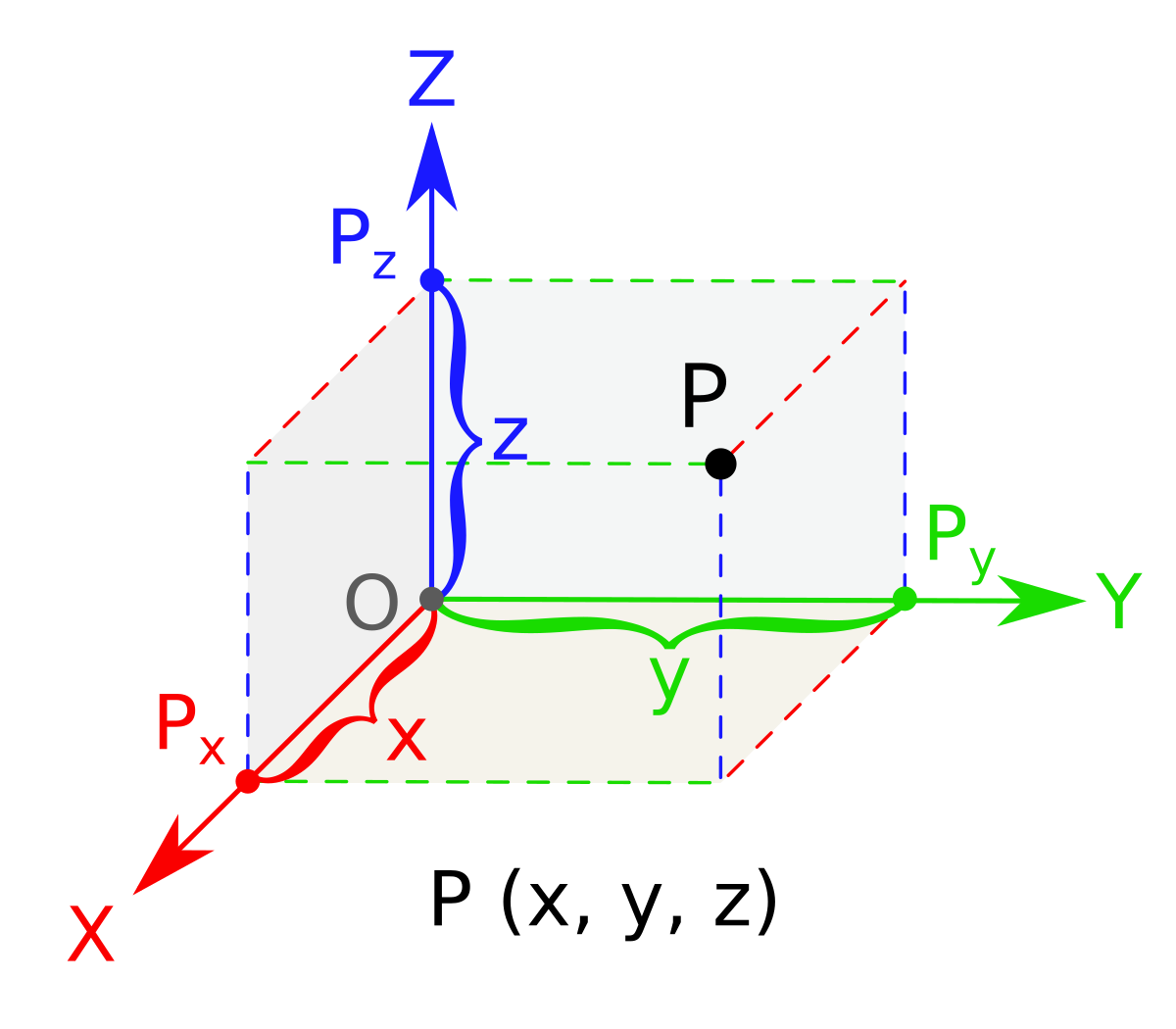
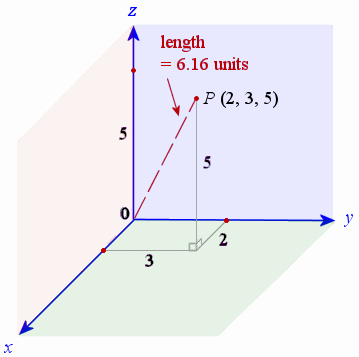
The distance between two points in three dimensions is given by. D x 2 x 1 2 y 2 y 1 2 z 2 z 1 2. Distance between two points formula in 3d space. A special case is when the initial point is at the origin which reduces the distance formula to the form.
We could determine it using pythagoras theorem as seen previously but we first need to find the value of d using values a and b. Distance of any point qxyz in space from origin o000 is given by. D x 1 x 0 2 y 1 y 0 2 z 1 z 0 2. Y y 0 m x x 0.
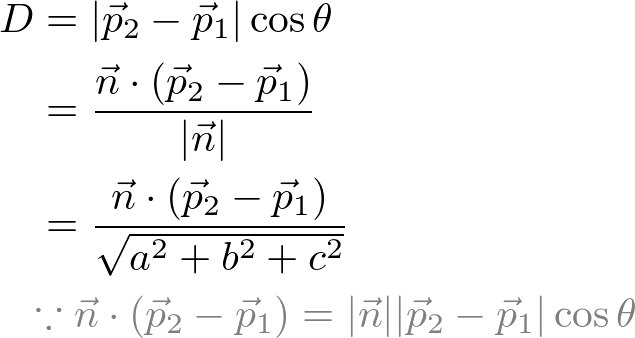

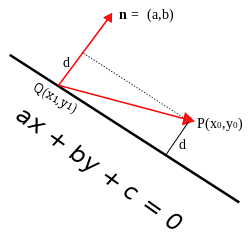





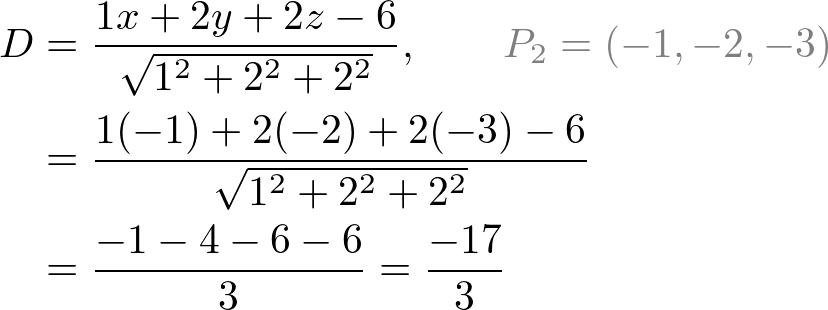
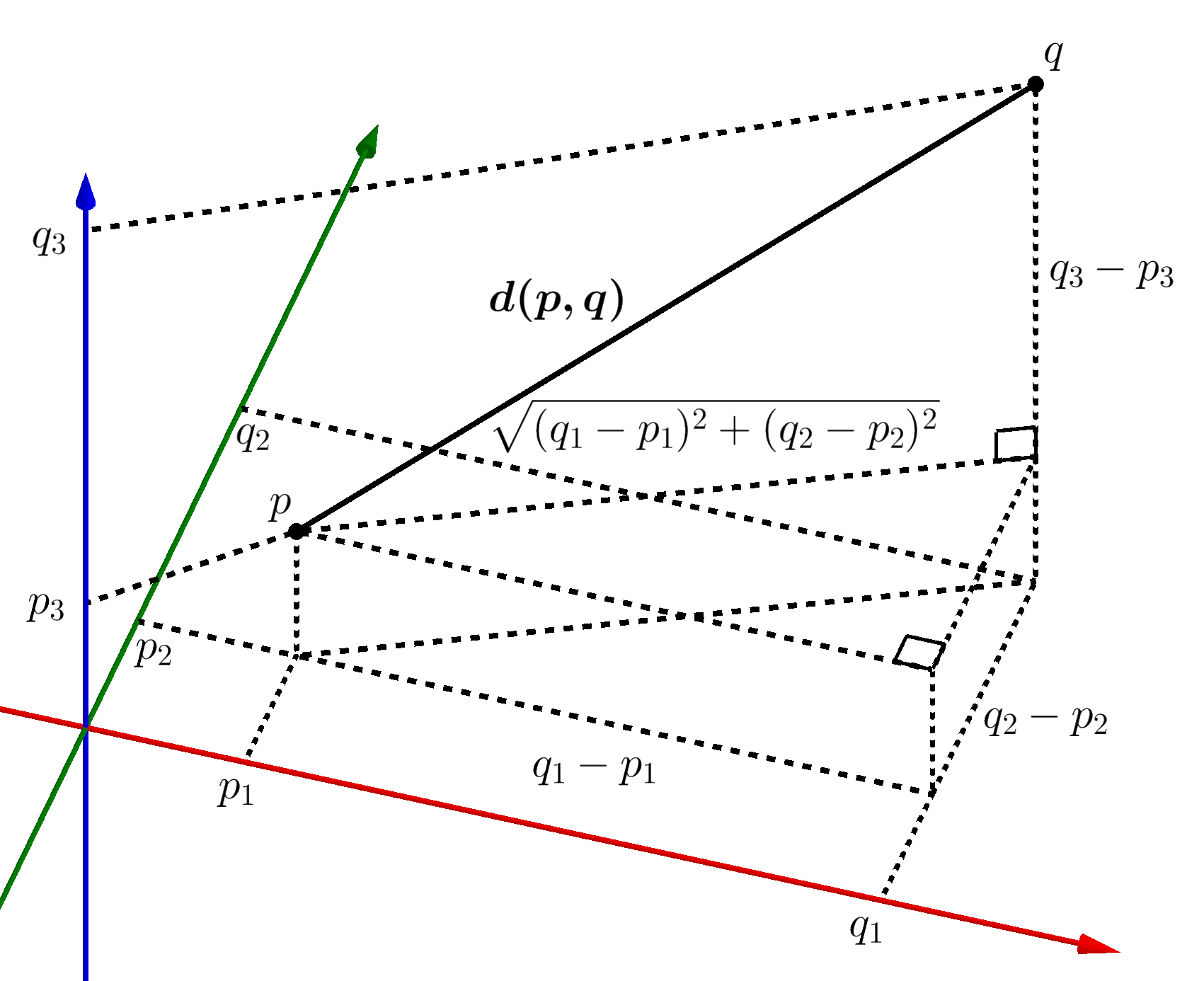
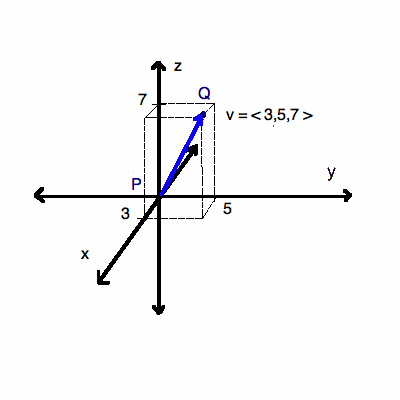




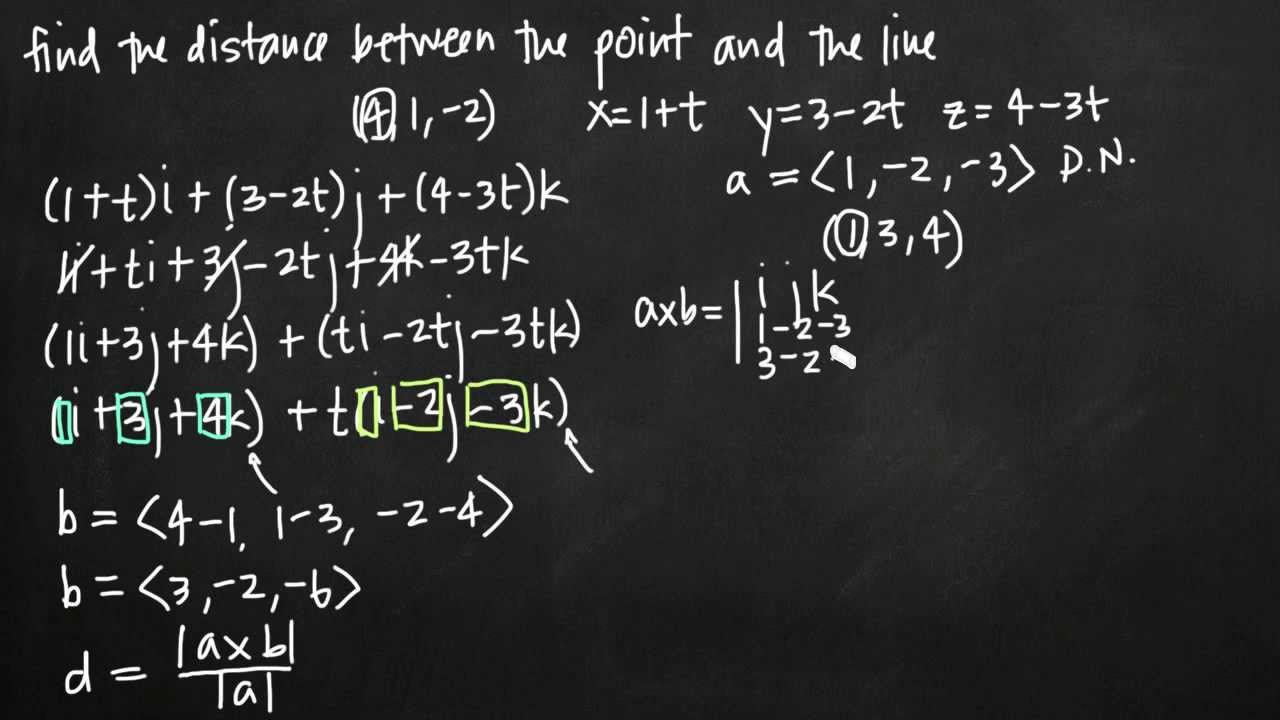


































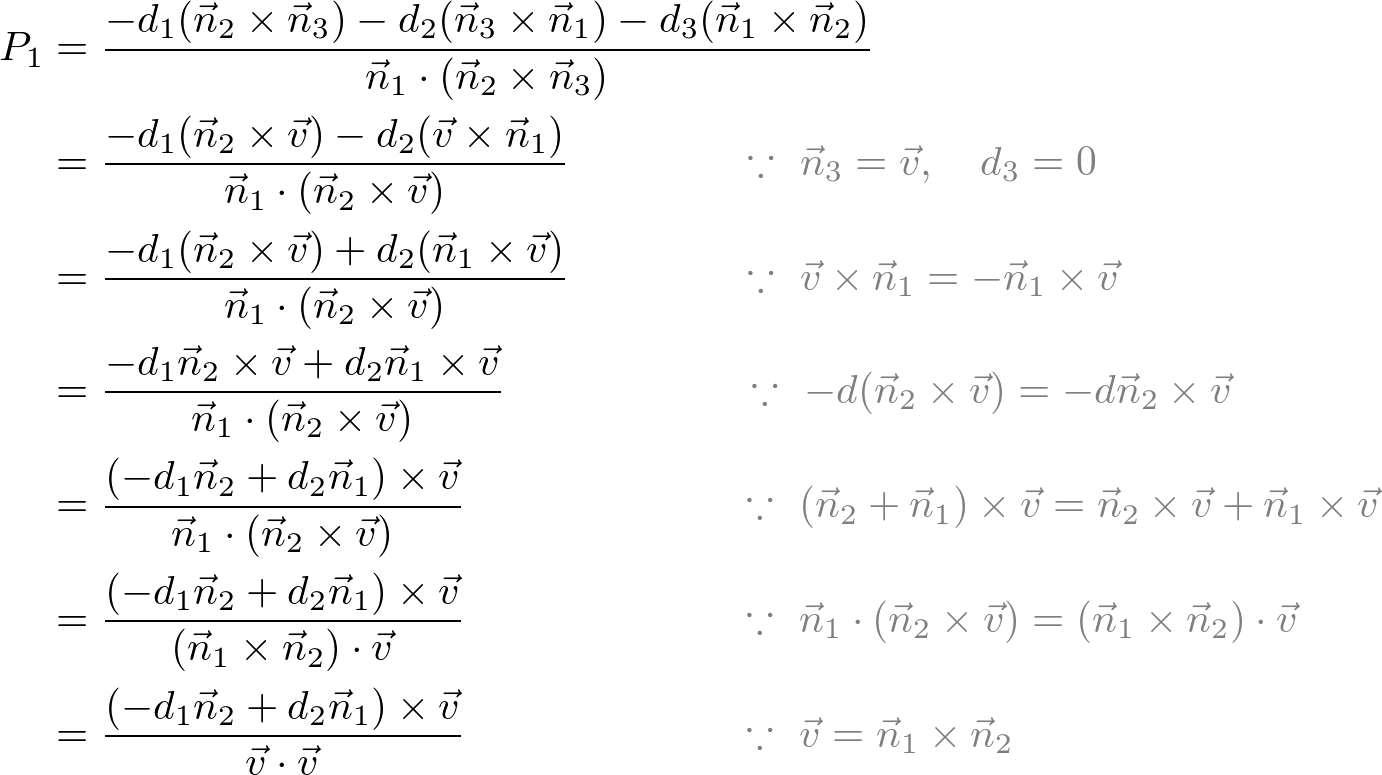


-space--with-Cartesian-coordinates-221.png)