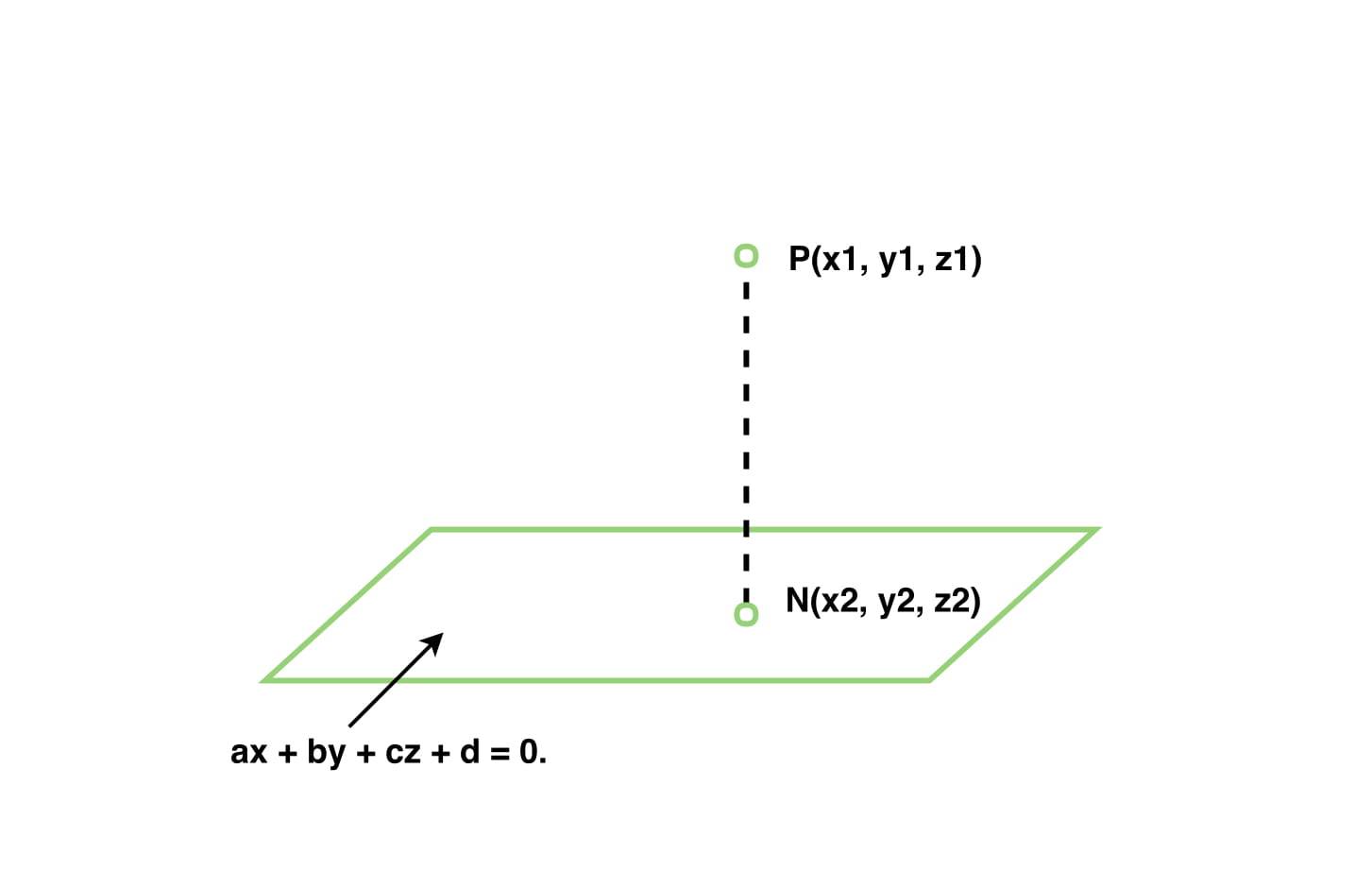
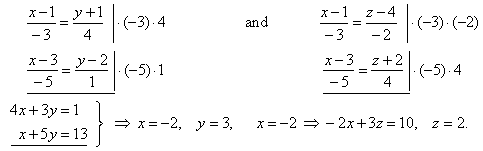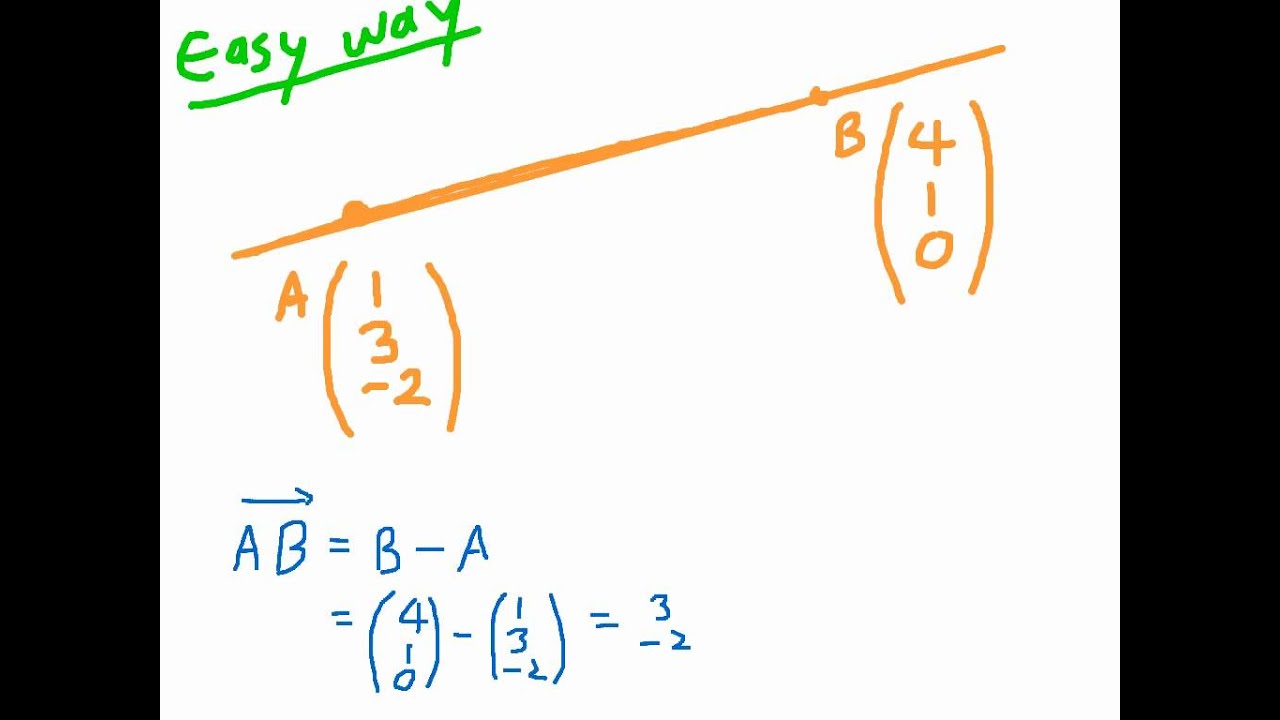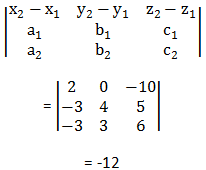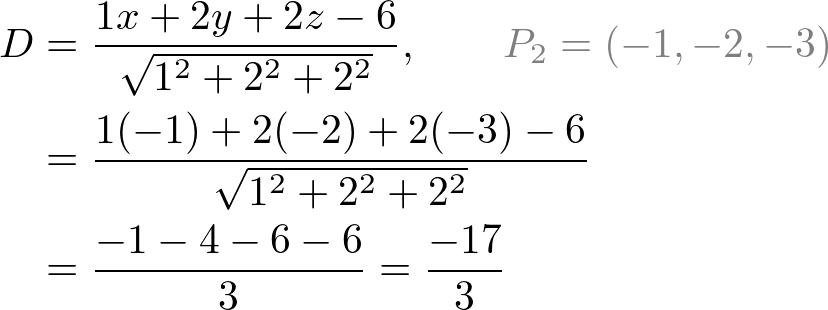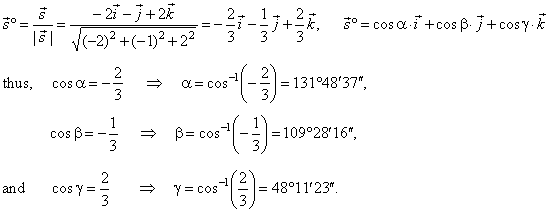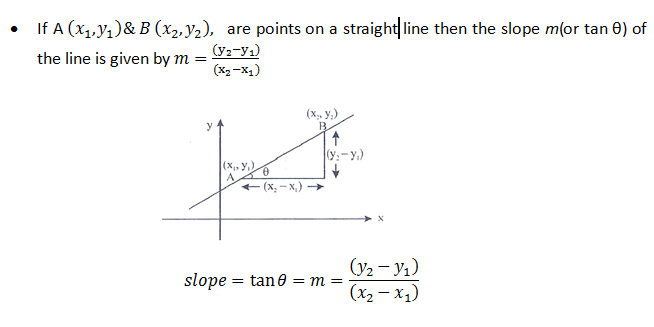Equation Of A Line In 3d From Two Points

For two known points we have two equations in respect to a and b. D p q 2 0 2. From this we can get the parametric equations of the line.
equation of a line in 3d from two points

Finding equation of a line in 3d.

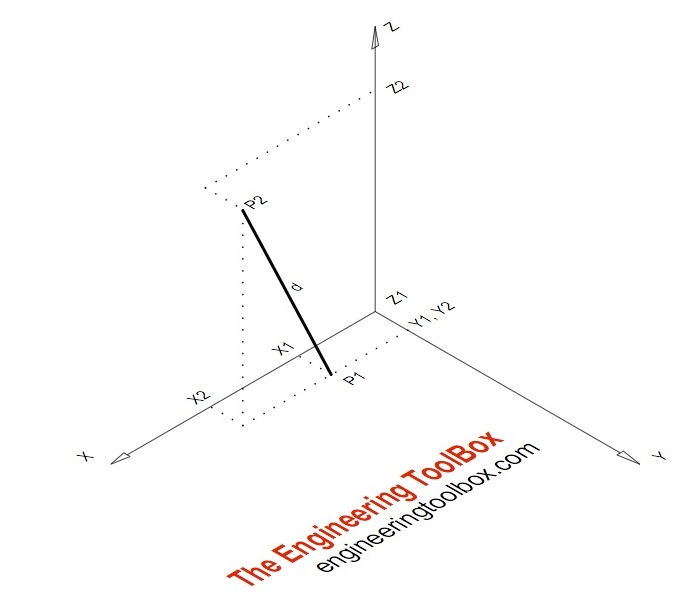
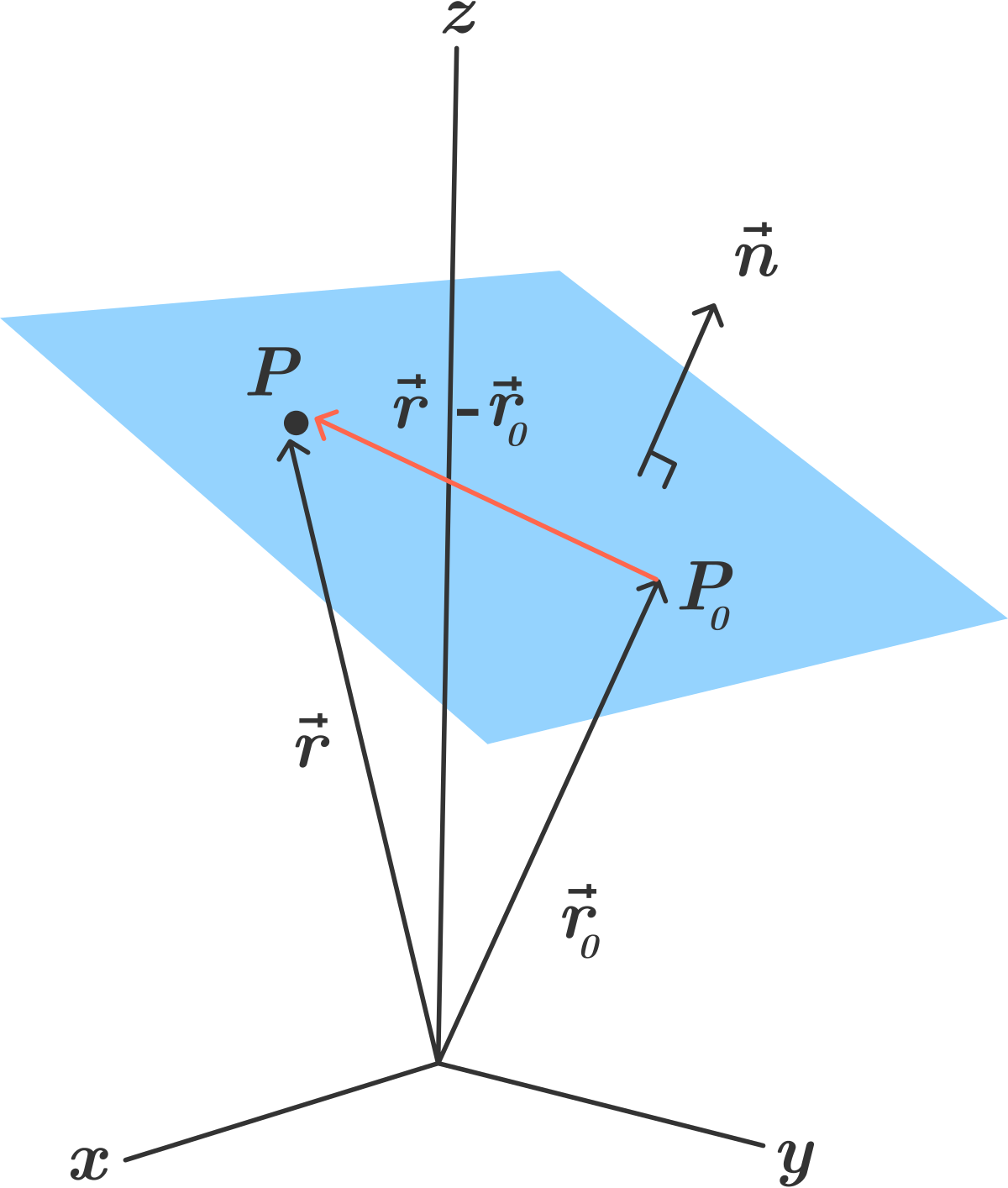
Equation of a line in 3d from two points. Z z2 z1 y2 y1 y y1 z1. Maths learning centre uofa 23680 views. B find a point on the line that is located at a distance of 2 units from the point 3 1 1. Analytical geometry line in 3d space.

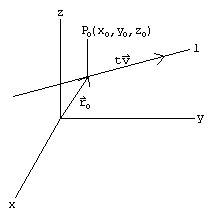
Line in 3d is determined by a point and a directional vector. X x 0 x 1 x 0 y y 0 y 1 y 0 z z 0 z 1 z 0. One may take this equal to parameter t r to use the parameteric equation of that line which is. Lets find out parametric form of line equation from the two.

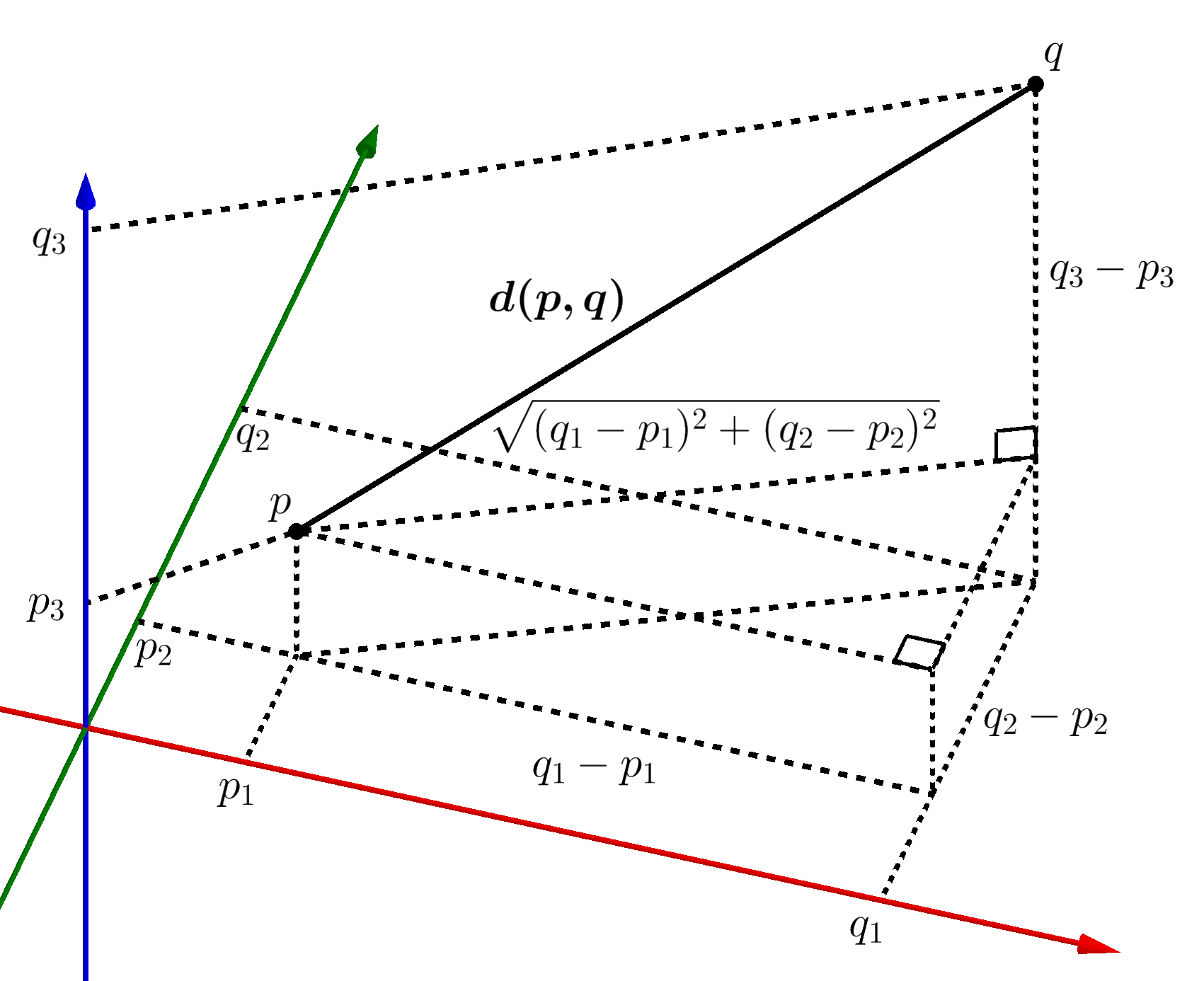
Lets subtract the first from the second and from there. Find the equation of the line that passes through the two points. D p q. Also if x1x2 and y1y2 you have a line in the z direction parallel to the z axis where the x1 plane intersections the y1 plane or at the x1y1 point.

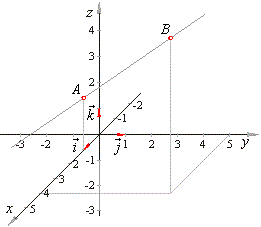
Vecr veca alpha vecb veca if the three dimensional coordinates of the points a and b are given as x 1 y 1 z 1 and x 2 y 2 z 2 then considering the rectangular co ordinates of point r as x y z. If we solve each of the parametric equations for t and then set them equal we will get symmetric equations of the line. Q 1 1 3. Find a the parametric equations of the line passing through the points p 1 3 1 1 and p 2 3 0 2.

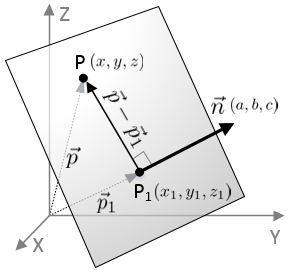
P 1 1 1 p 111 p 111 and. Note that b can be expressed like this so once we have a it is easy to calculate b simply by plugging or to the expression above. So the equation of your line is simple any z point with xx1 and yy1. Therefore the vector equation of a line passing through two given points is given by.

The directional vector can be found by subtracting coordinates of second point from the coordinates of first point. With points a x 0 y 0 z 0 and b x 1 y 1 z 1 the canonical equation of a line passes through theses points is. Finding the equation of a line in 3d through two points duration. Vec dvec pq 202.

Subtracting the position vectors of the two points gives the direction vector which is. Vector and parametric equations of a line. X x 1 x 0 t x 0 y y 1 y 0 t y 0 z z 1 z 0 t z 0.