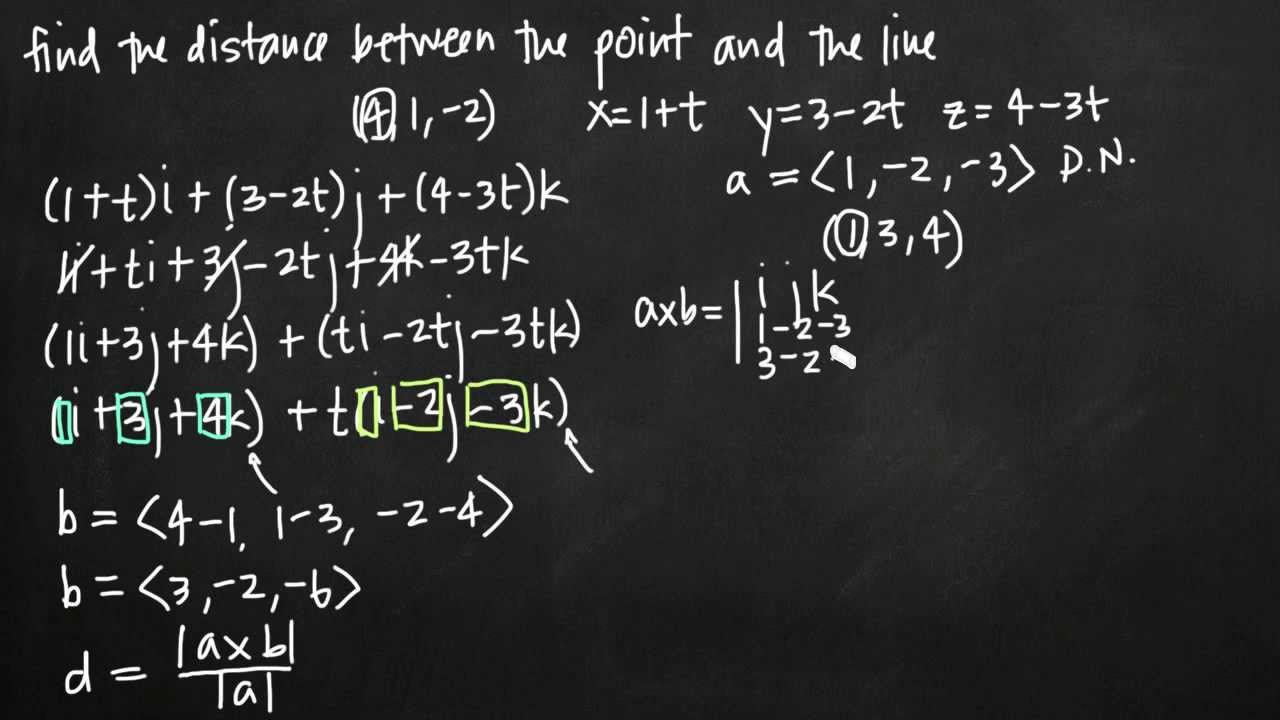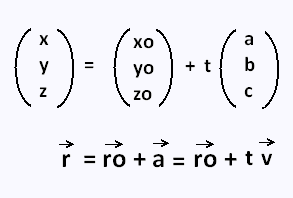Equation Of A Line In 3d Space

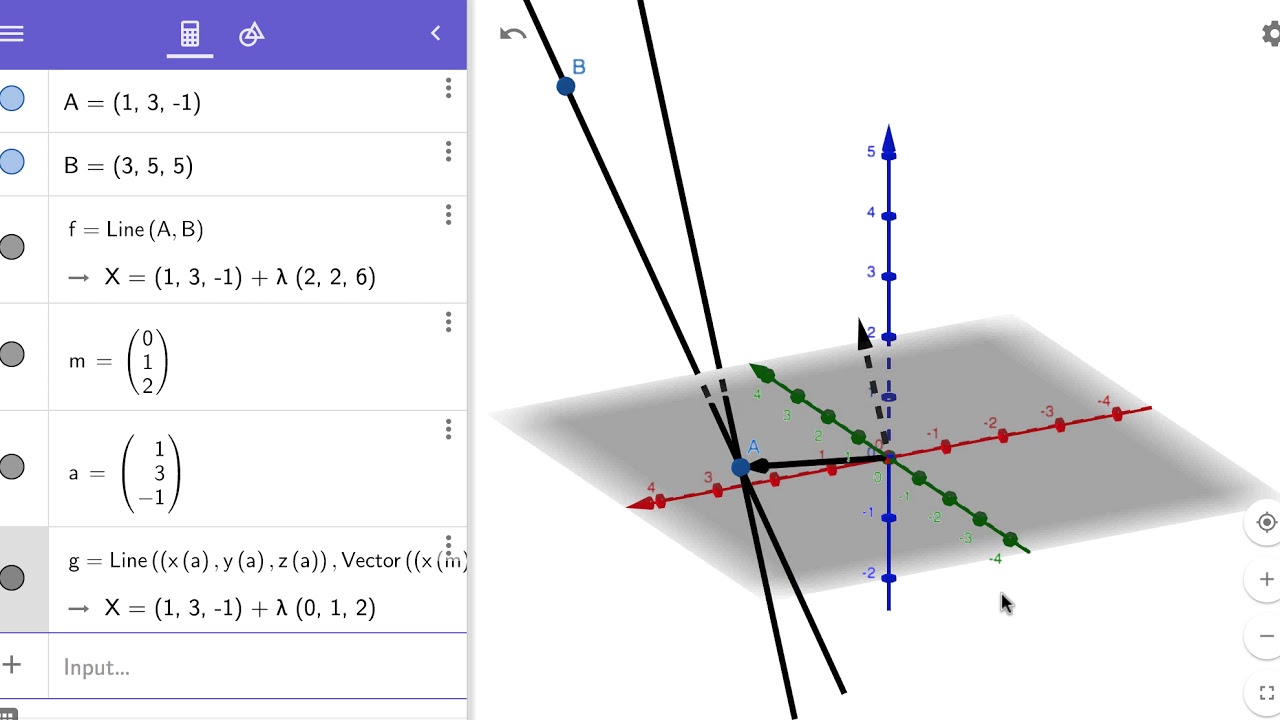
X 2 1 y 1 5 z 3 6 x 2 1 y 1 5 z 3 6.

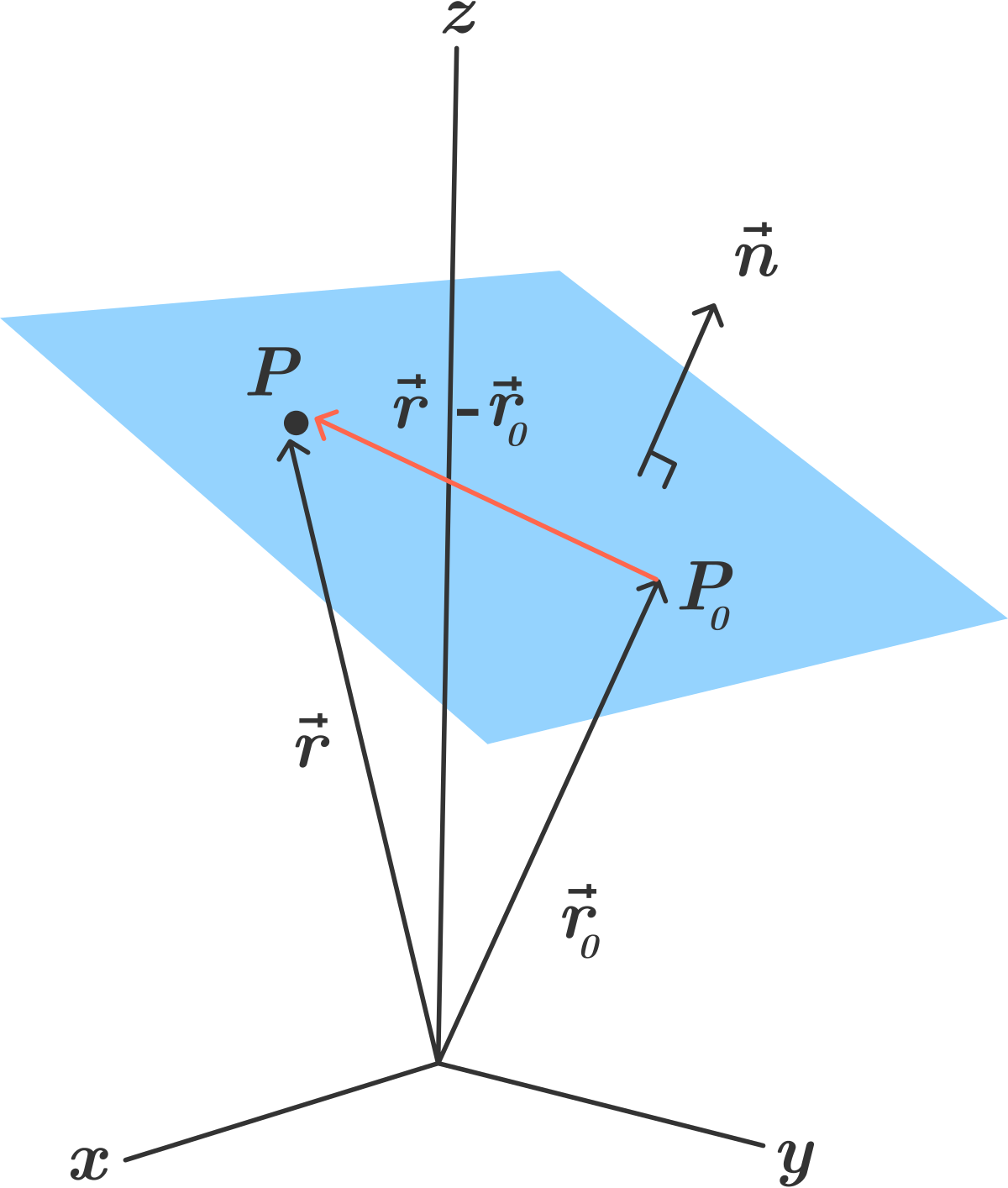
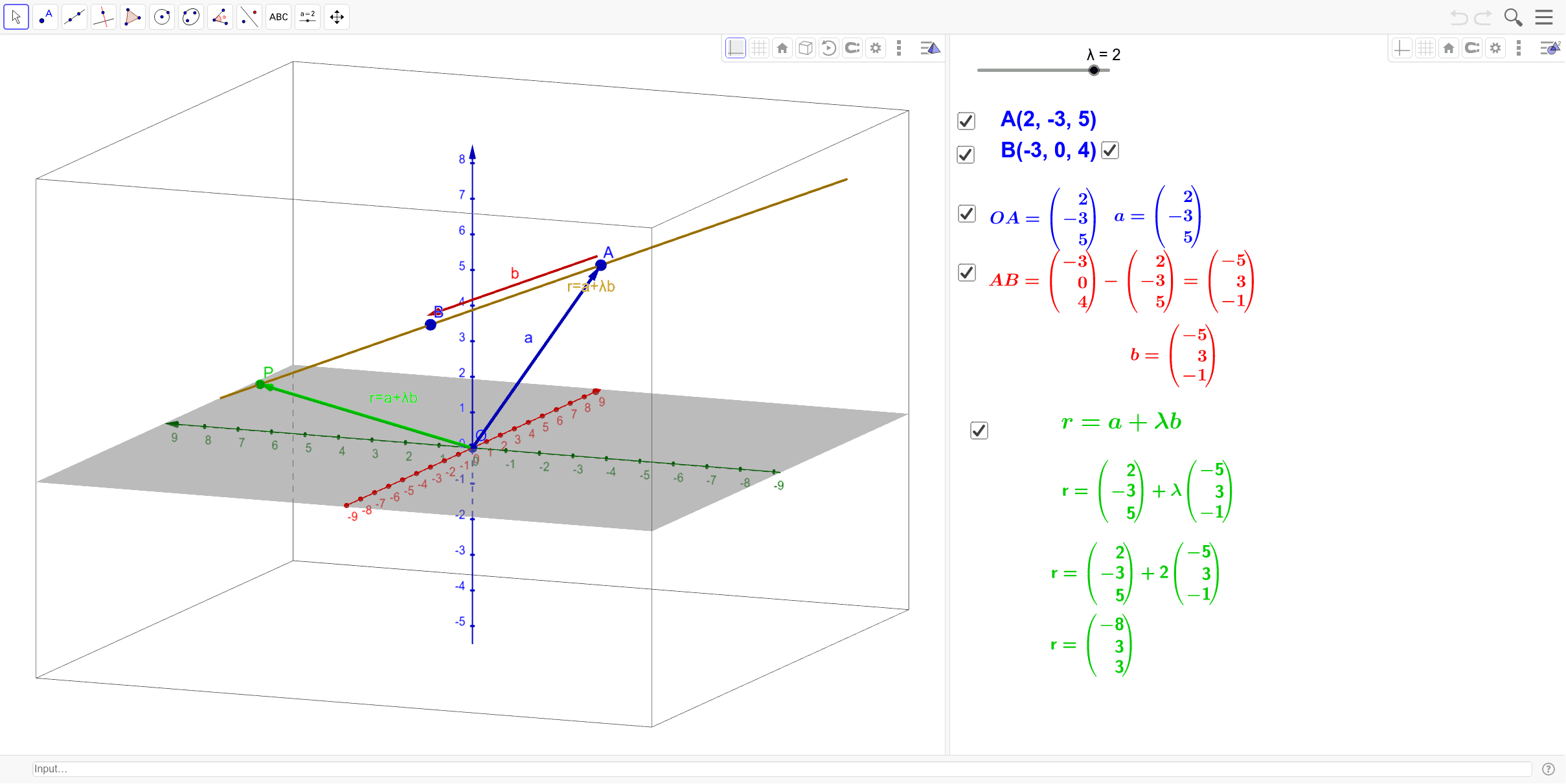
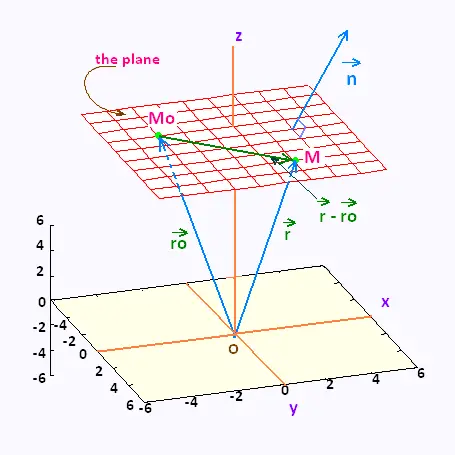
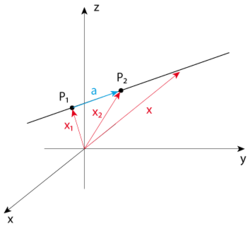
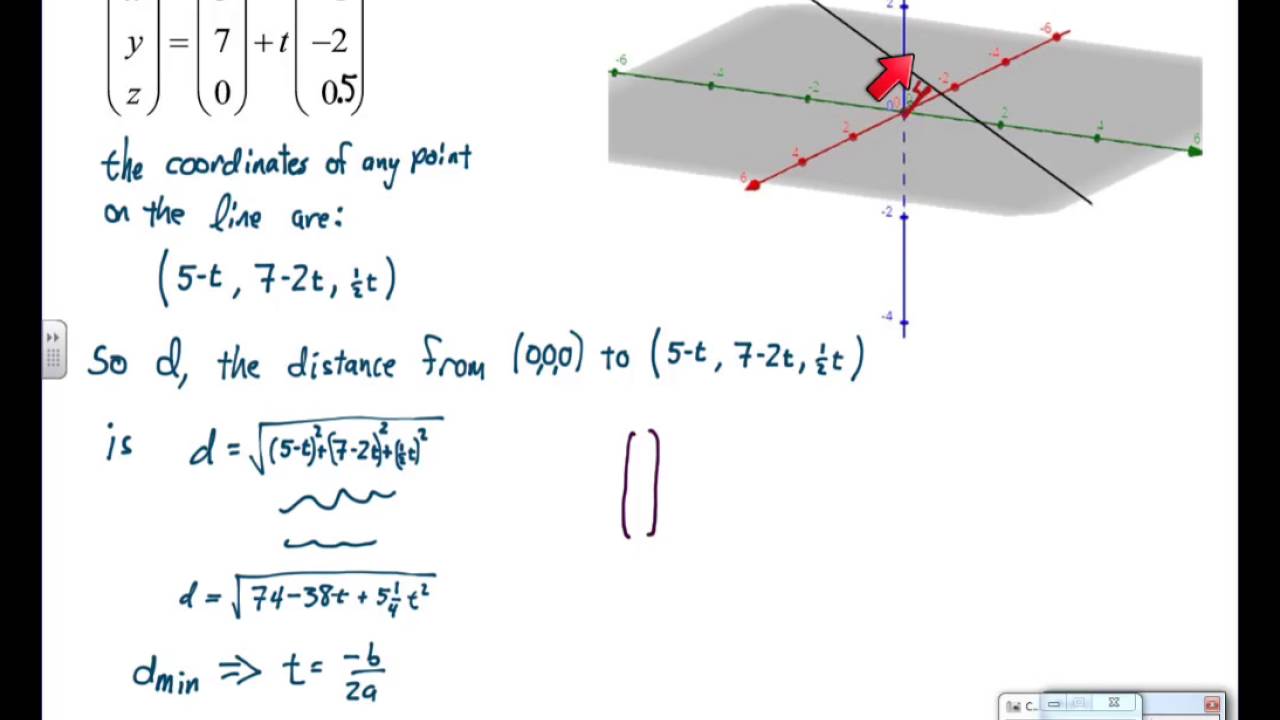
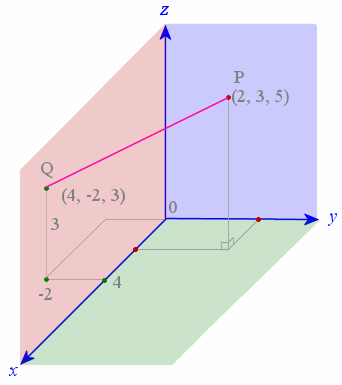
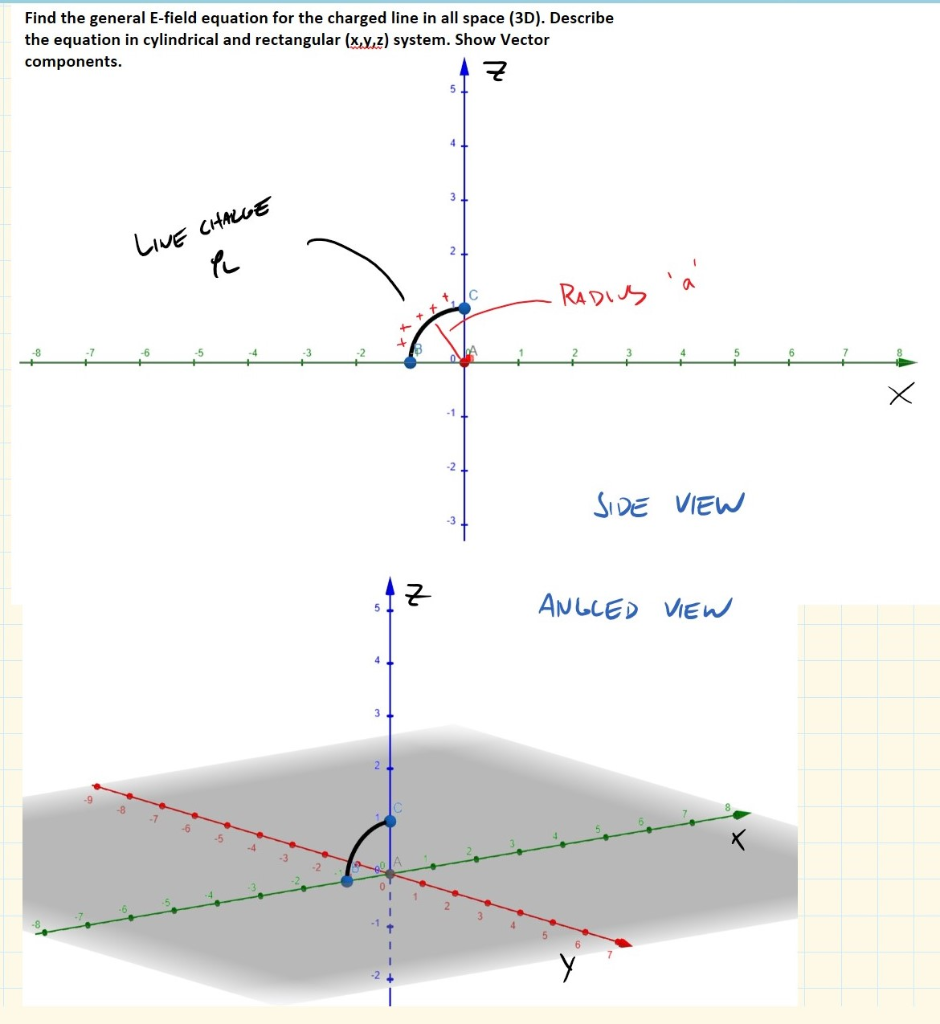
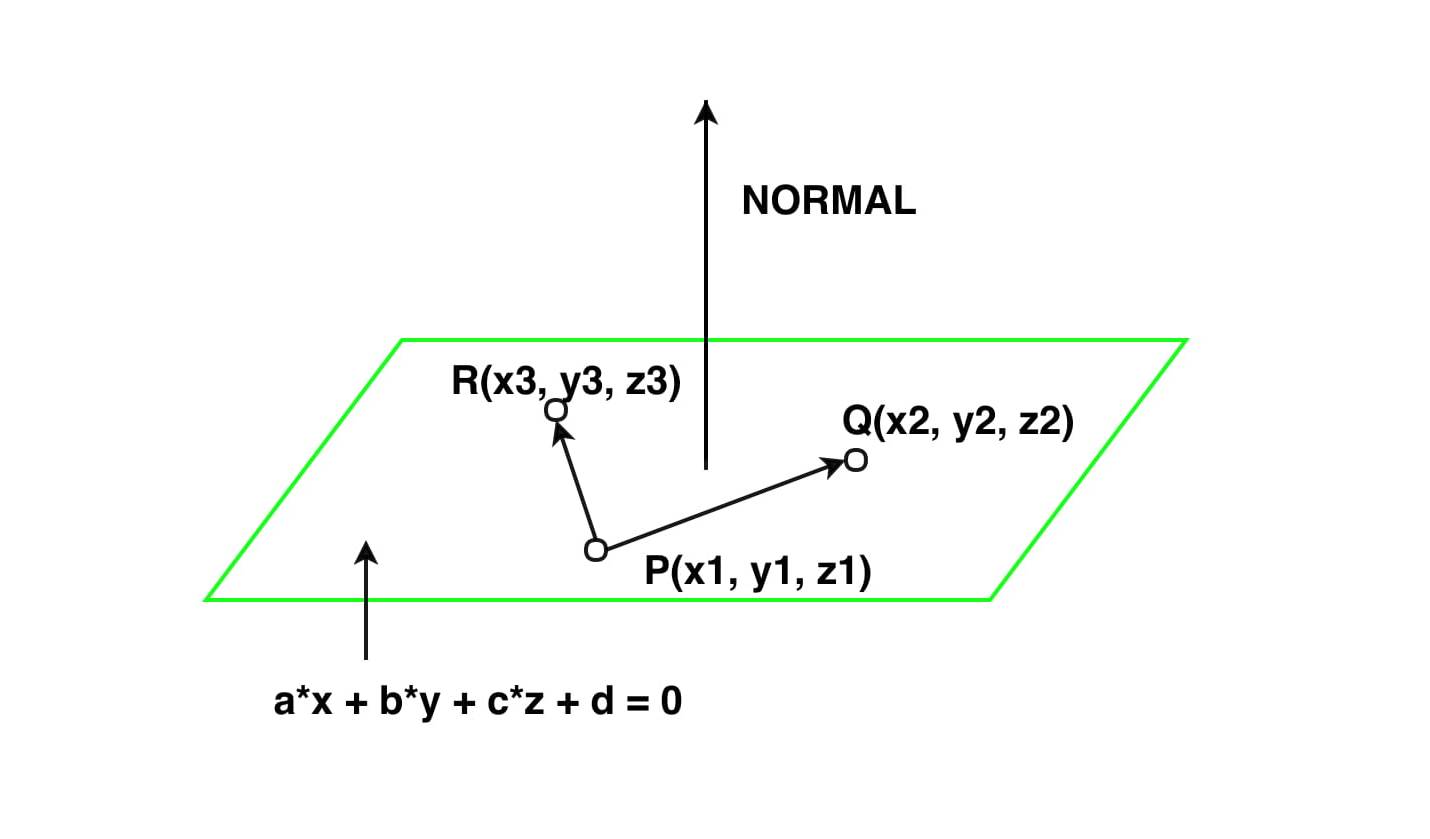
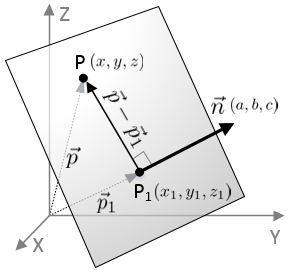
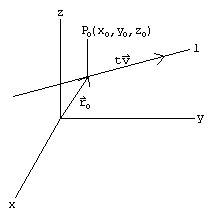
Equation of a line in 3d space. B find a point on the line that is located at a distance of 2 units from the point 3 1 1. Here is the symmetric form. Find a the parametric equations of the line passing through the points p 1 3 1 1 and p 2 3 0 2. Vector equation of a line the equation vecs rvecs r0tvecs v used to describe a line with direction vector vecs v abc passing through point px0y0z0 where vecs r0 x0y0z0 is the position vector of point p vector equation of a plane.

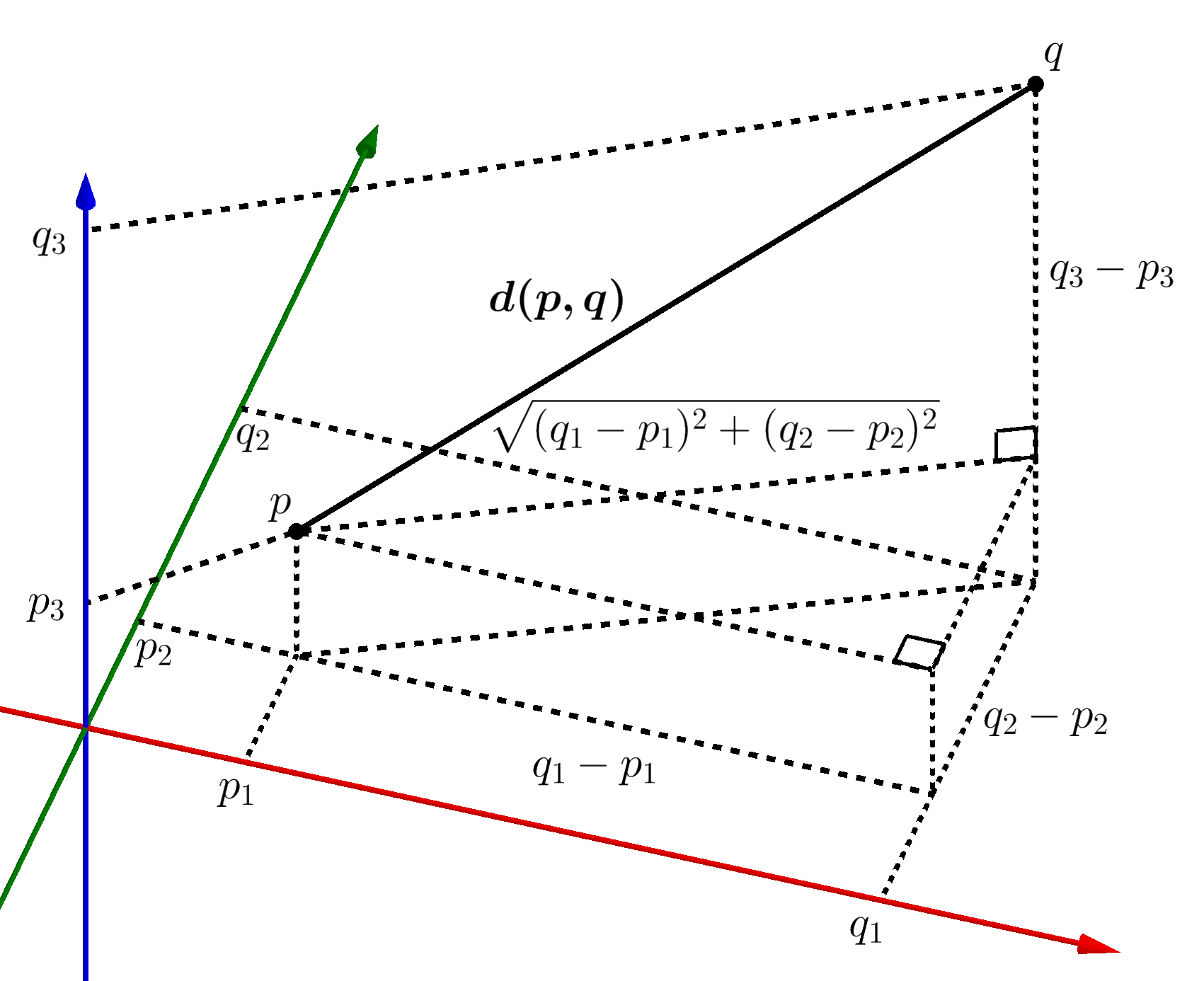
We must however look at how the equation of a line is written in vector form and cartesian form. Equation of a line in space equation of the line passing through two different points in space if the line passes through two points ax1 y1 z1 and bx2 y2 z2 such that x1 x2 y1 y2and z1 z2 then equation of linecan be found using the following formula x x1. If we take the vector equation. Equation of a line in three dimensions equation of a line is defined as y mxc where c is the y intercept and m is the slope.

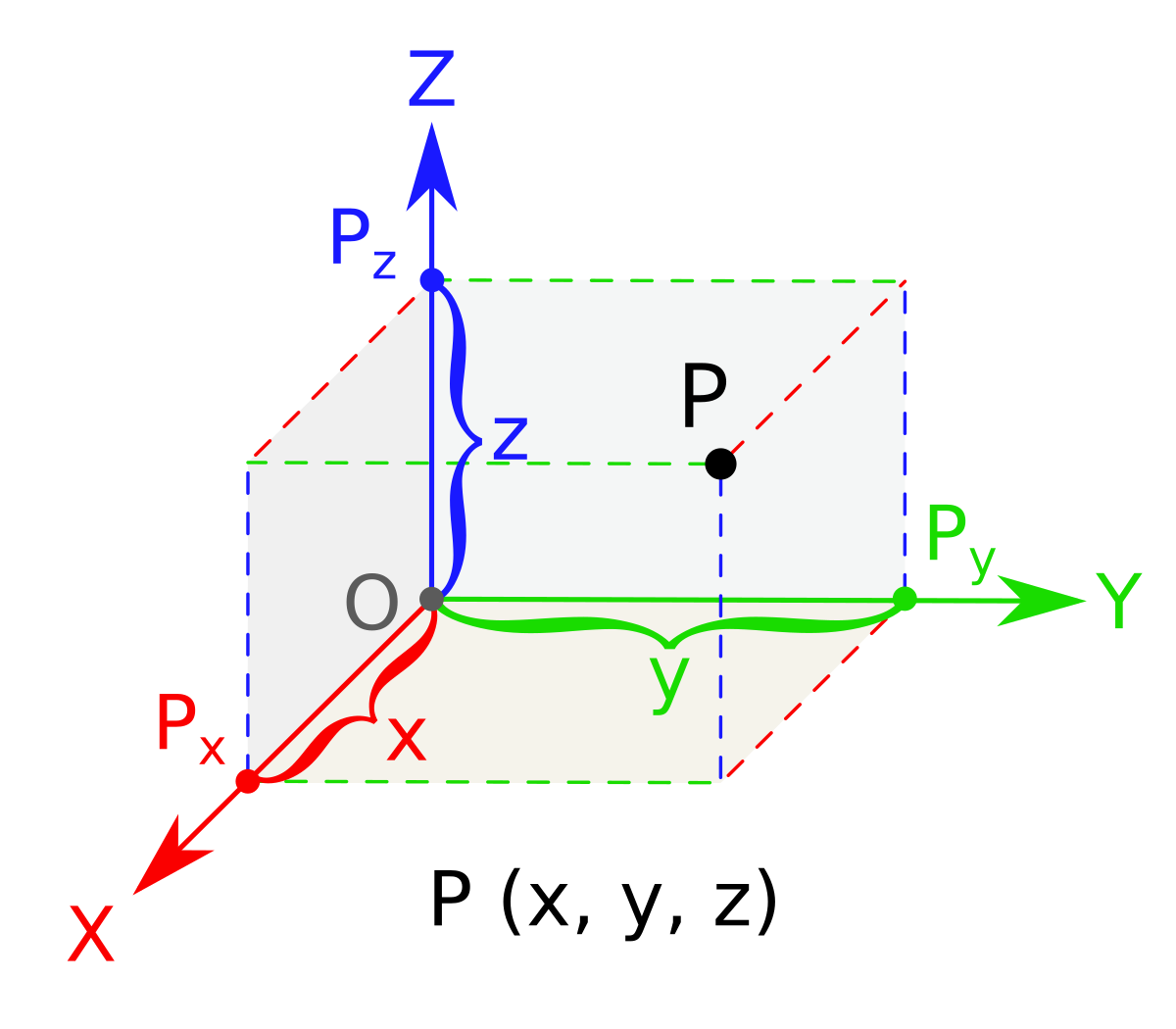
Analytical geometry line in 3d space. Vectors can be defined as a quantity possessing both direction and magnitude. This lesson equation of line explains how the equation of a line in 3 d space can be found. Symmetric equations if we solve for tin equation 110 assuming that a6 0 b6 0 and c6 0 we obtain x x 0 a y y 0.

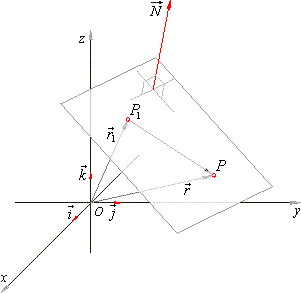
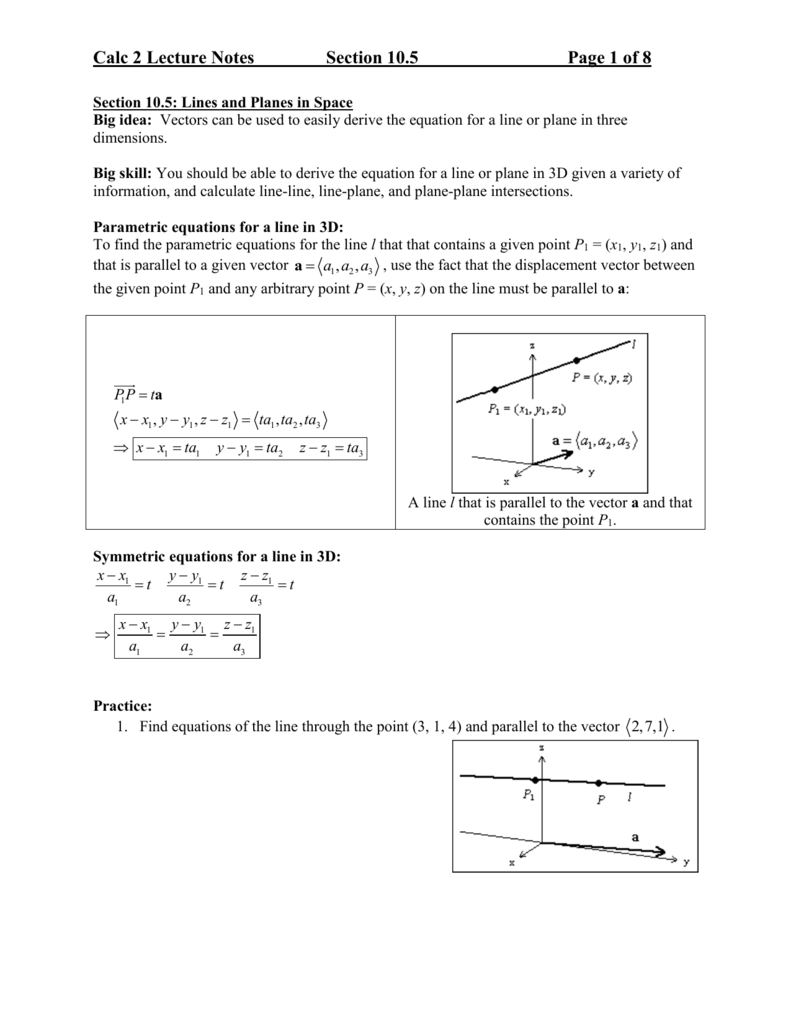
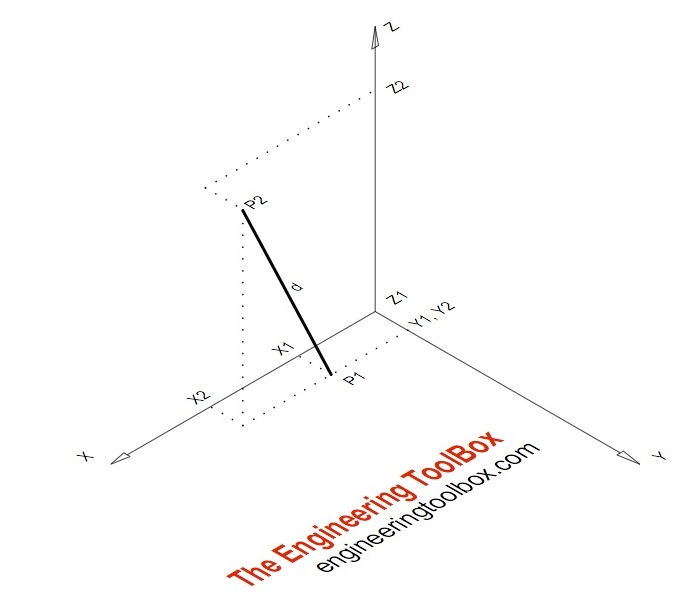
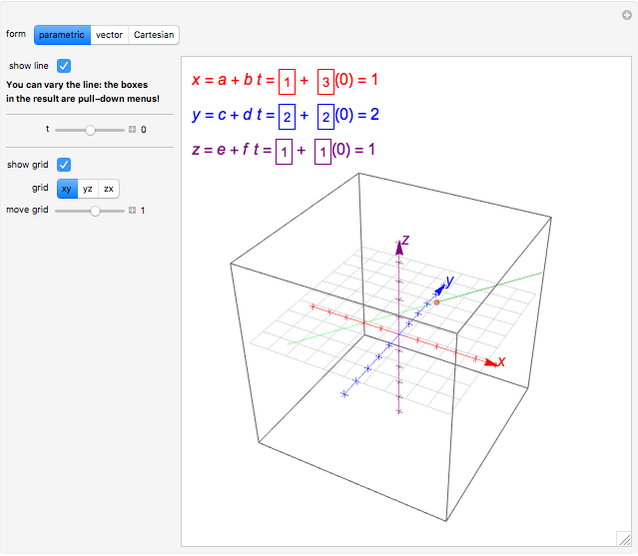
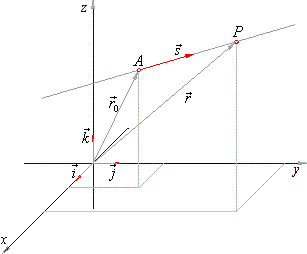
Similarly in three dimensional space we can obtain the equation of a line if we know a point that the line passes through as well as the direction vector which designates the direction of the line. The equation of a line with direction vector d l m n vecdlmn d l m n that passes through the point x 1 y 1 z 1 x1y1z1 x 1 y 1 z 1 is given by the formula. 0 ct 110 denition 67 equation 110 is known as the parametric equation of the line l. Here are the parametric equations of the line.

X 2 t y 1 5 t z 3 6 t x 2 t y 1 5 t z 3 6 t. Once we have this equation the other two forms follow.