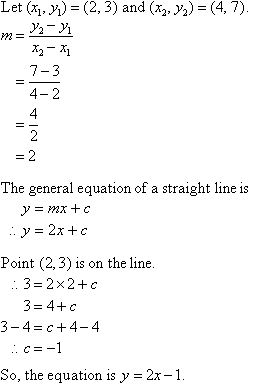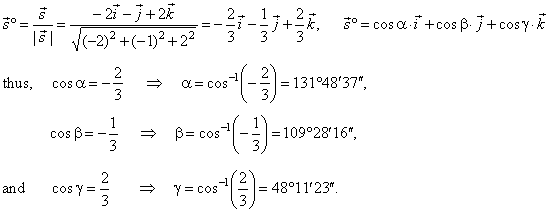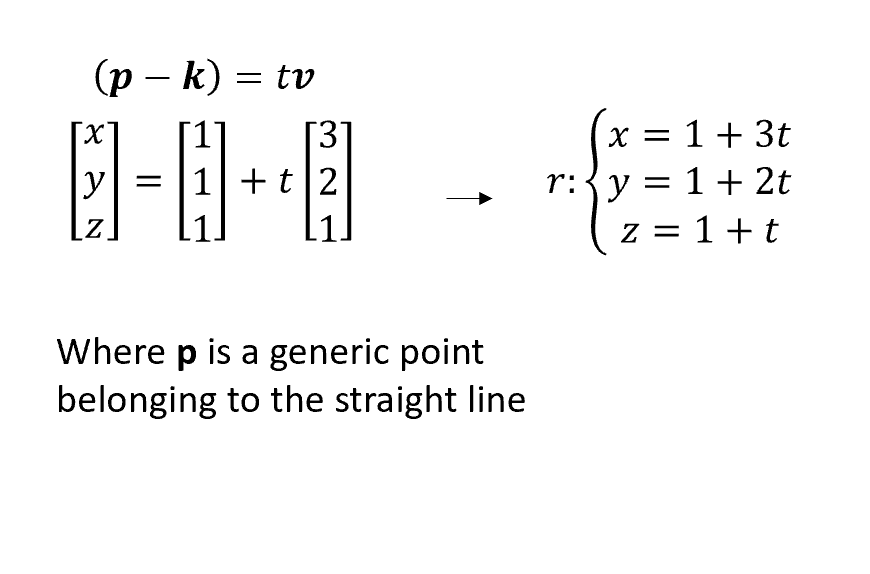Equation Of A Straight Line In 3d

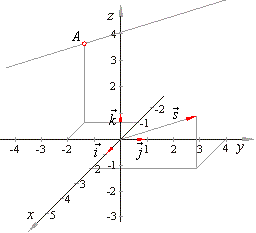
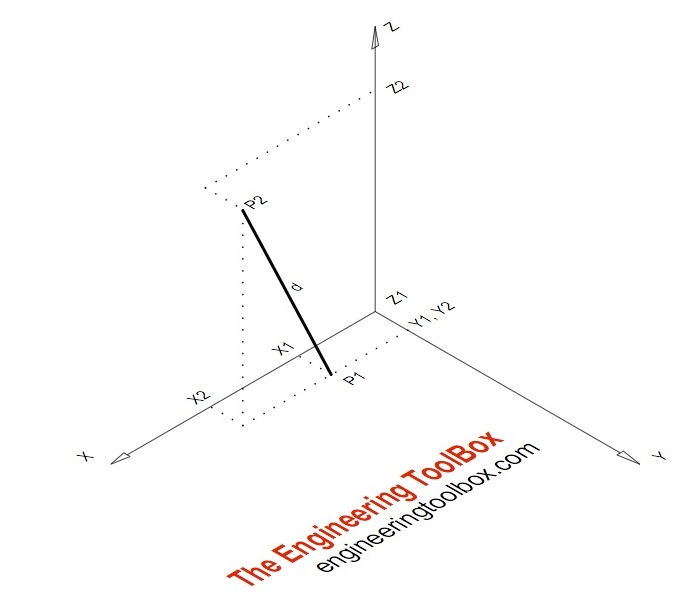
Draw a vector of length 1 starting at p1 and pointing toward p2.

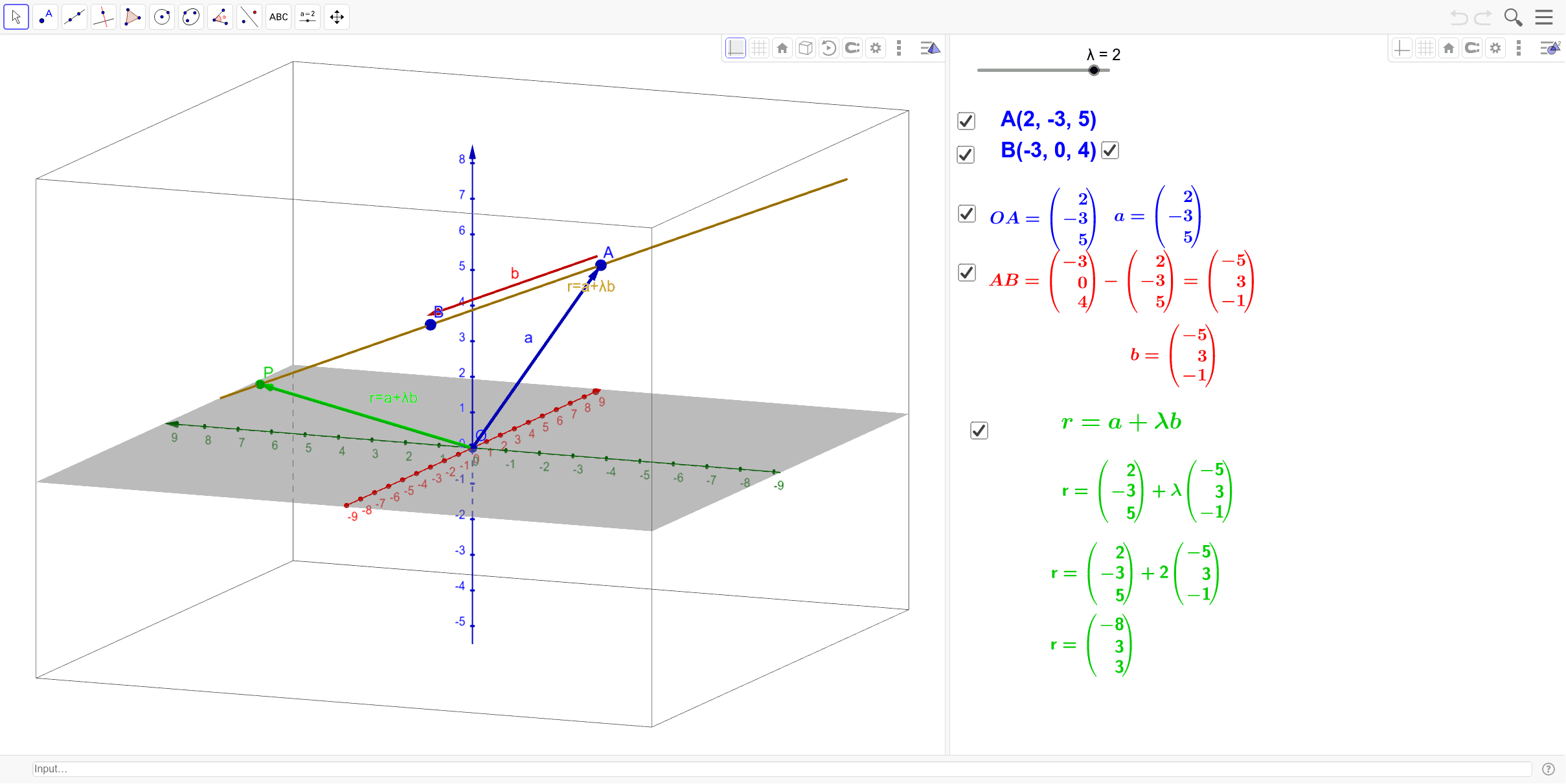
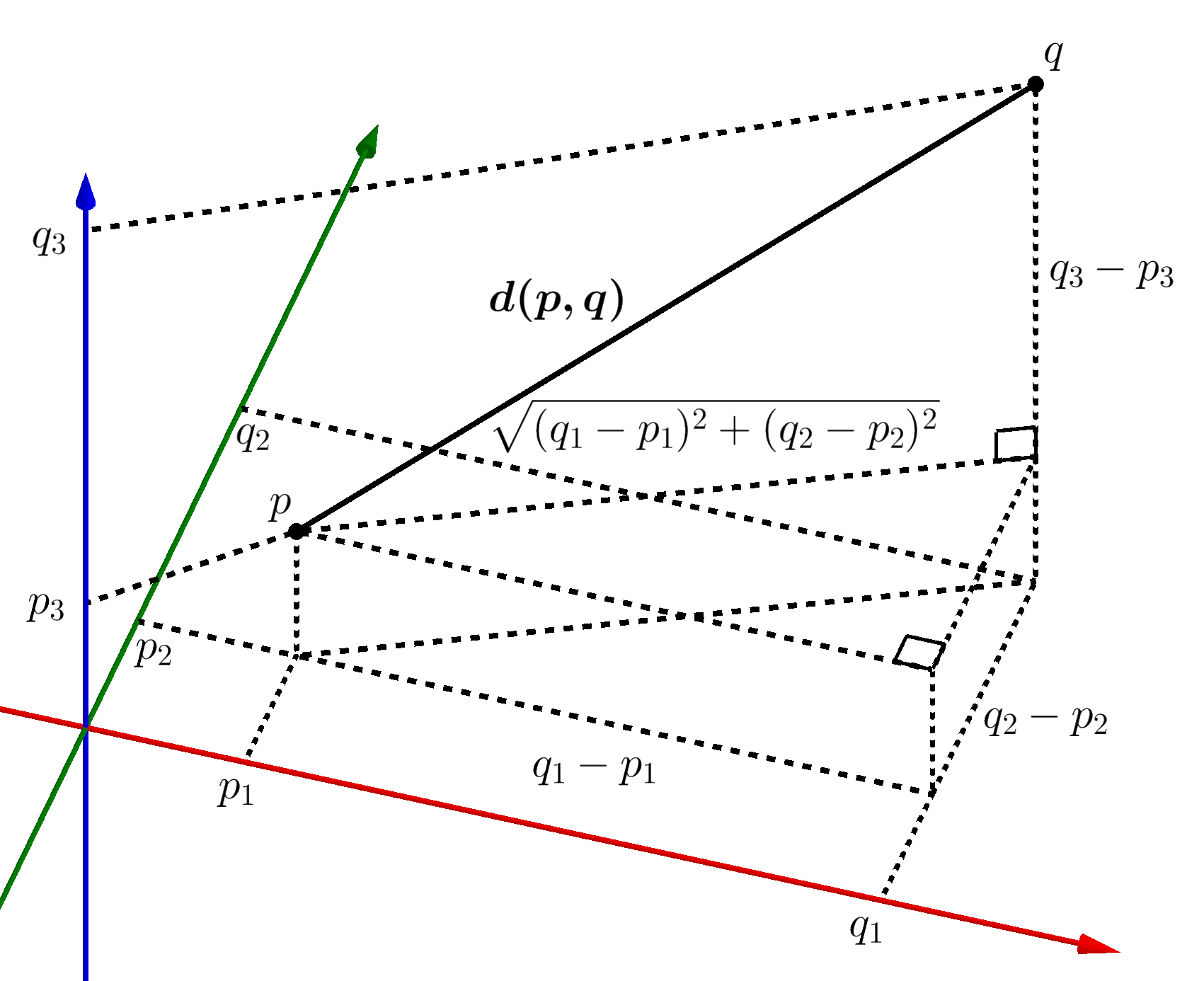
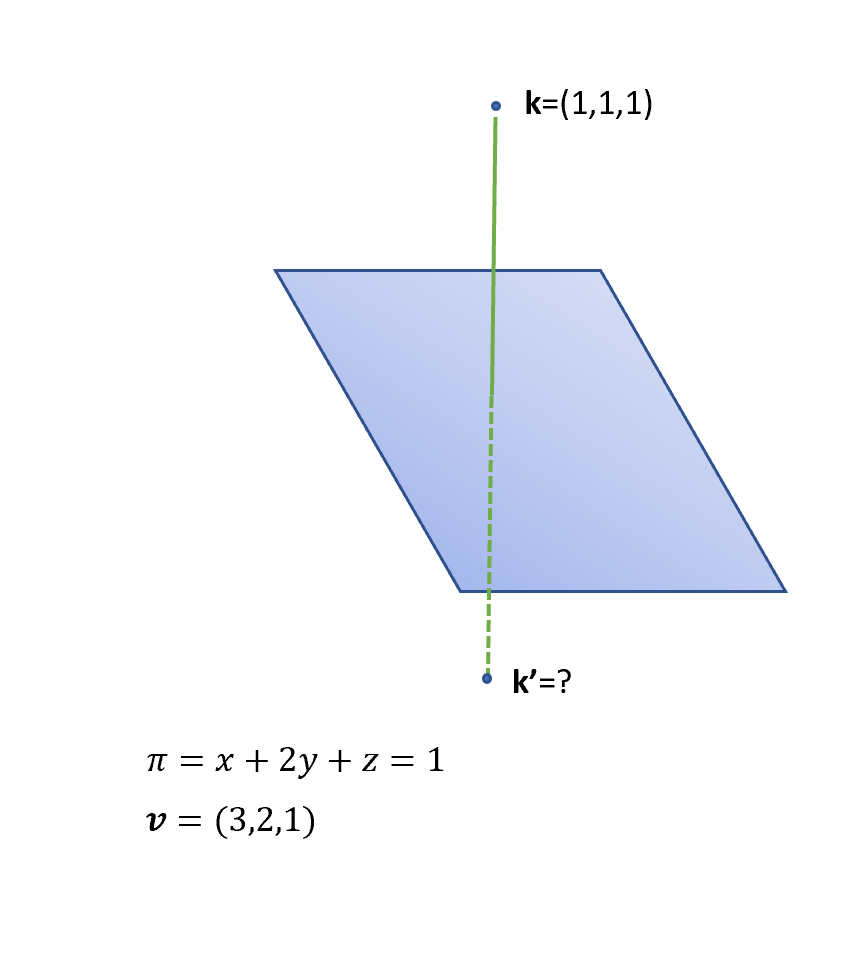
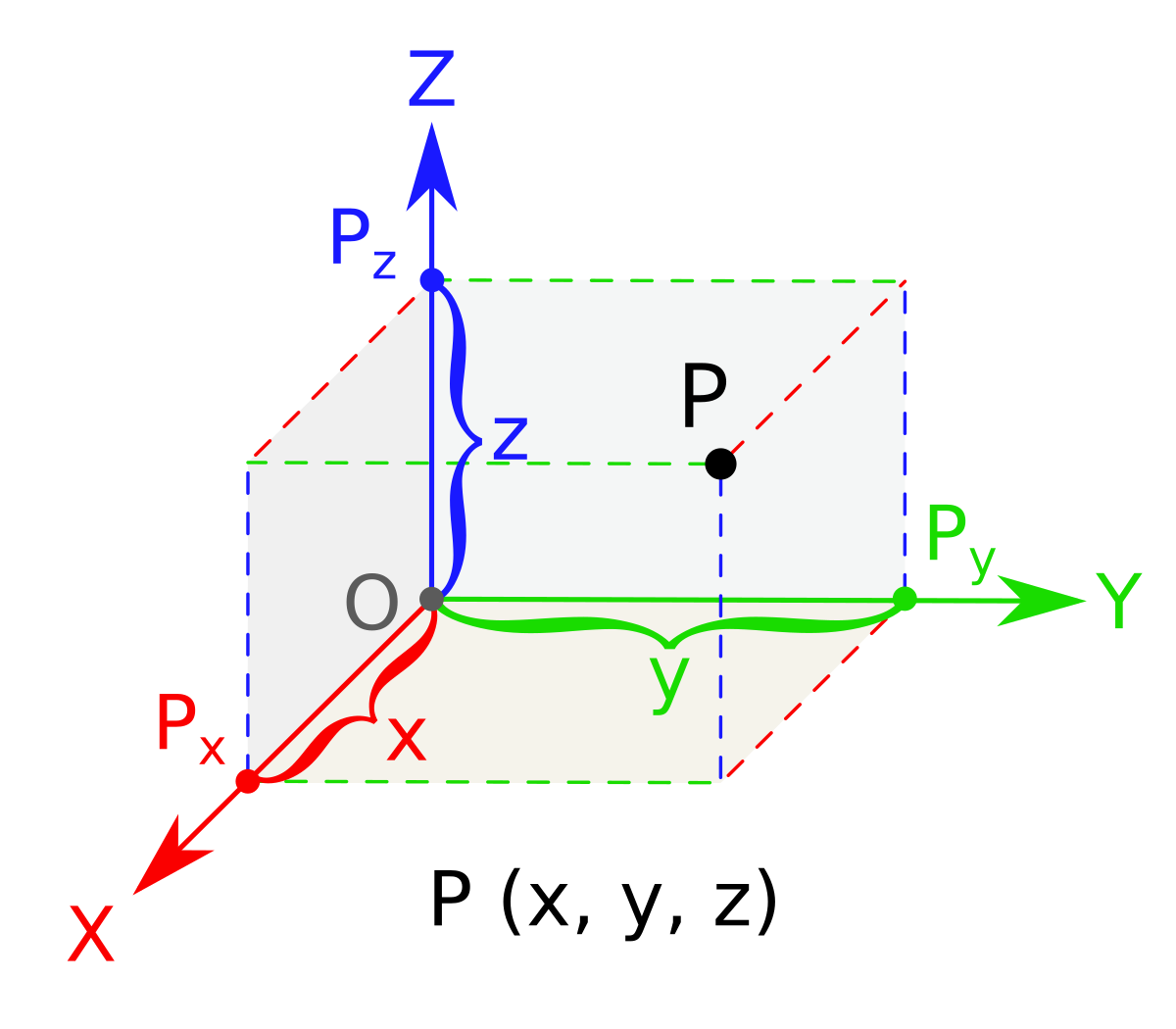
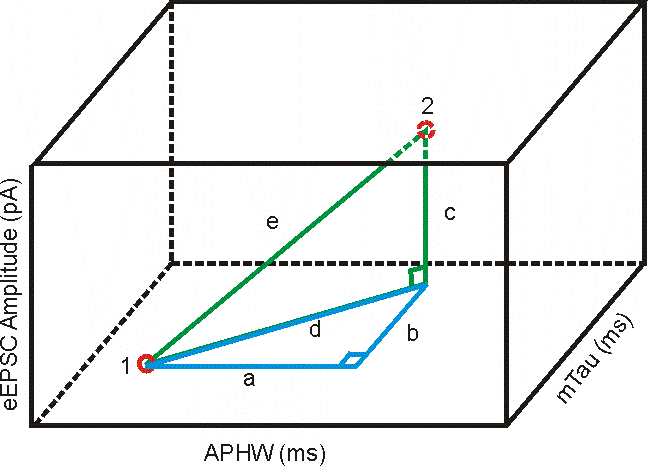
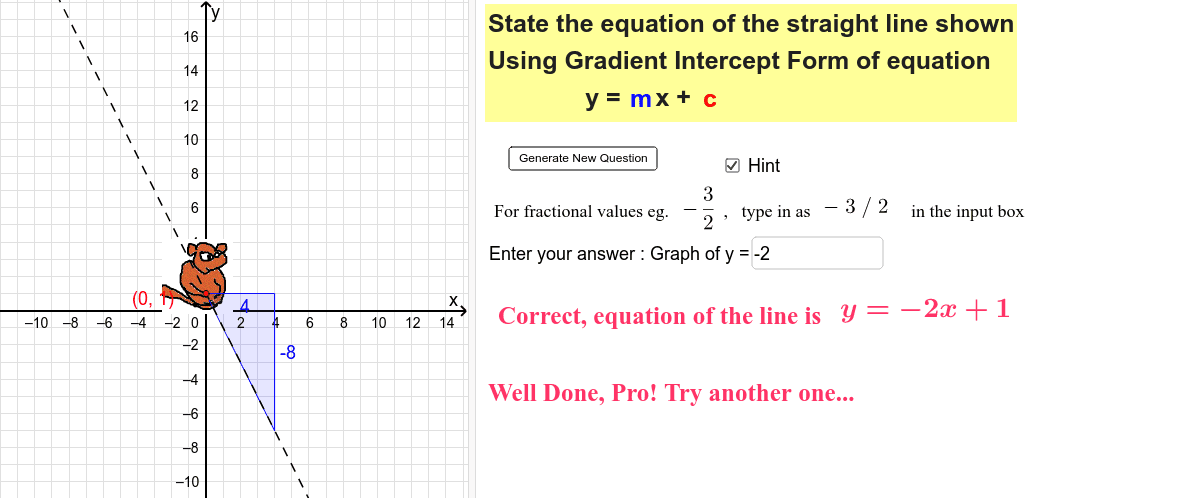
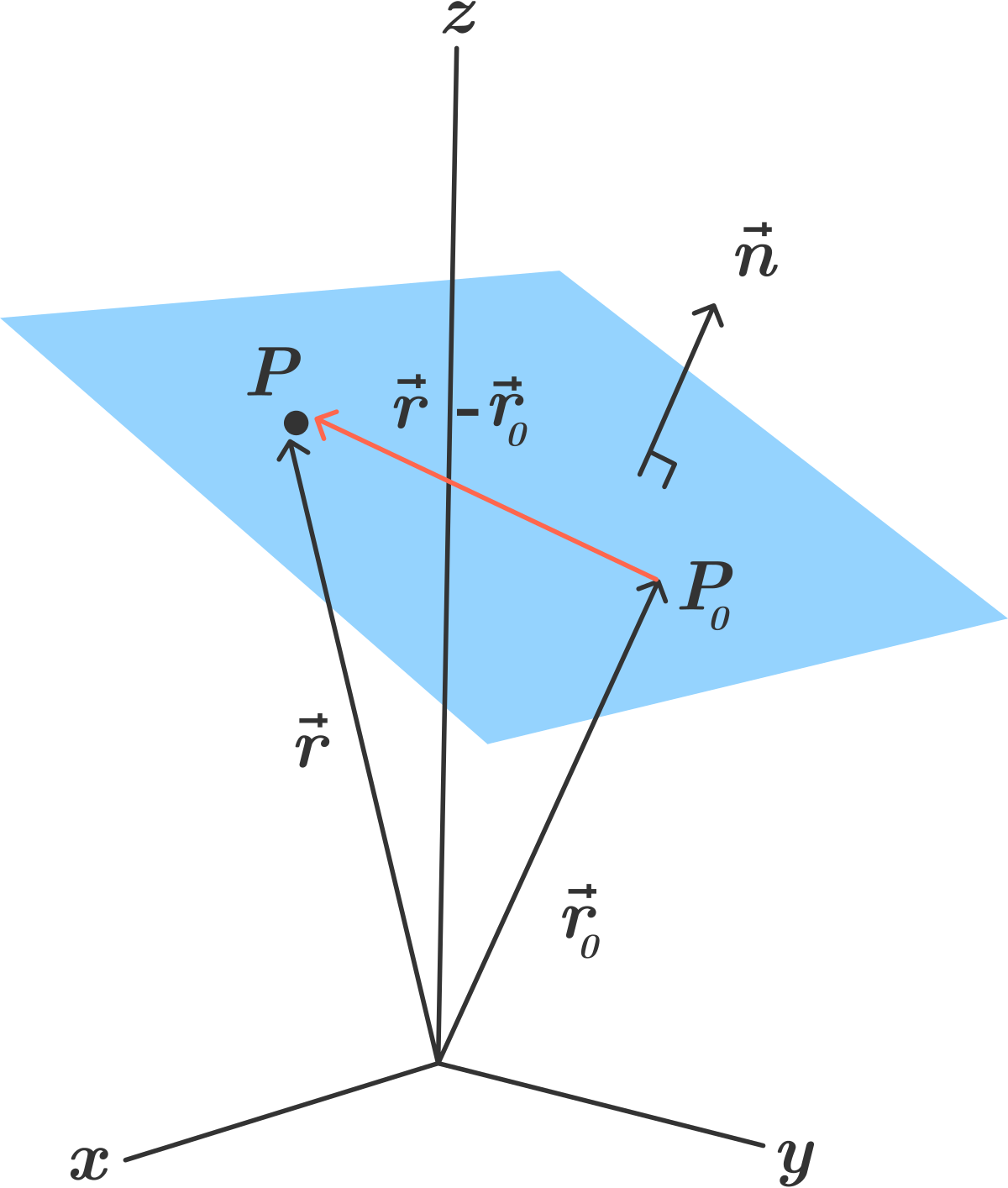
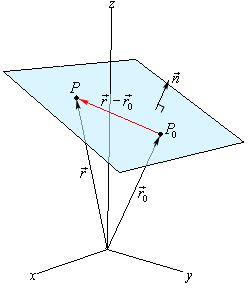
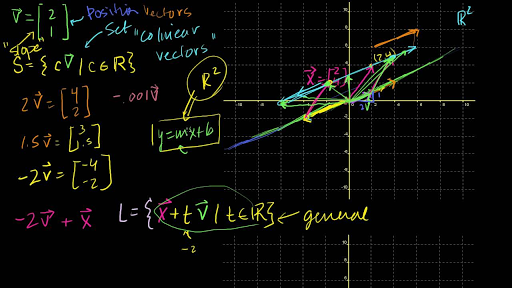
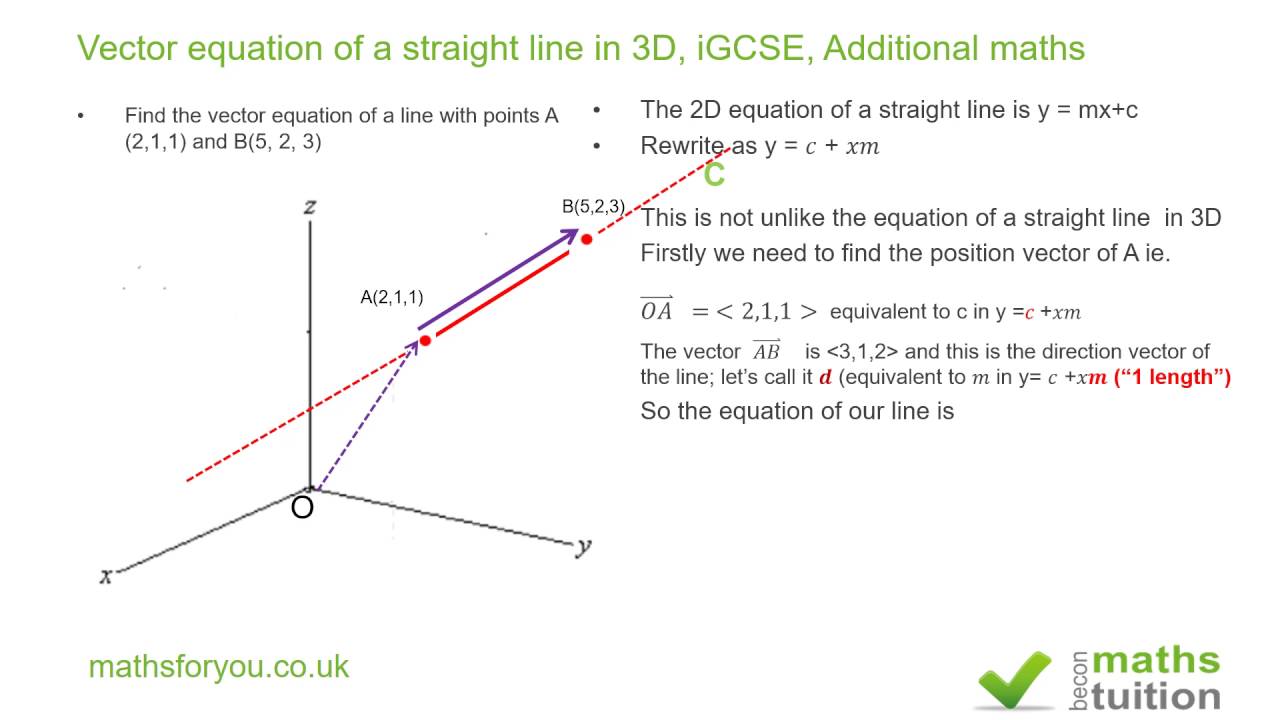
Equation of a straight line in 3d. General equation of straight line is a 1 x b 1 y c 1 z d 1 0 a 2 x b 2 y c 2 z d 2 0 1. The equation of a line in a plane is given by the popular equation y m x c. In three dimensional geometry a straight line is defined as the intersection of two planes. This lesson equation of line explains how the equation of a line in 3 d space can be found.

As far as d is concerned draw two points p1 and p2 separated by a distance of say 3. The formula is as follows. Varying d traces out the line. 5 r v2 for given air conditions shape and inclination of the object we must determine a value for cd to determine drag.

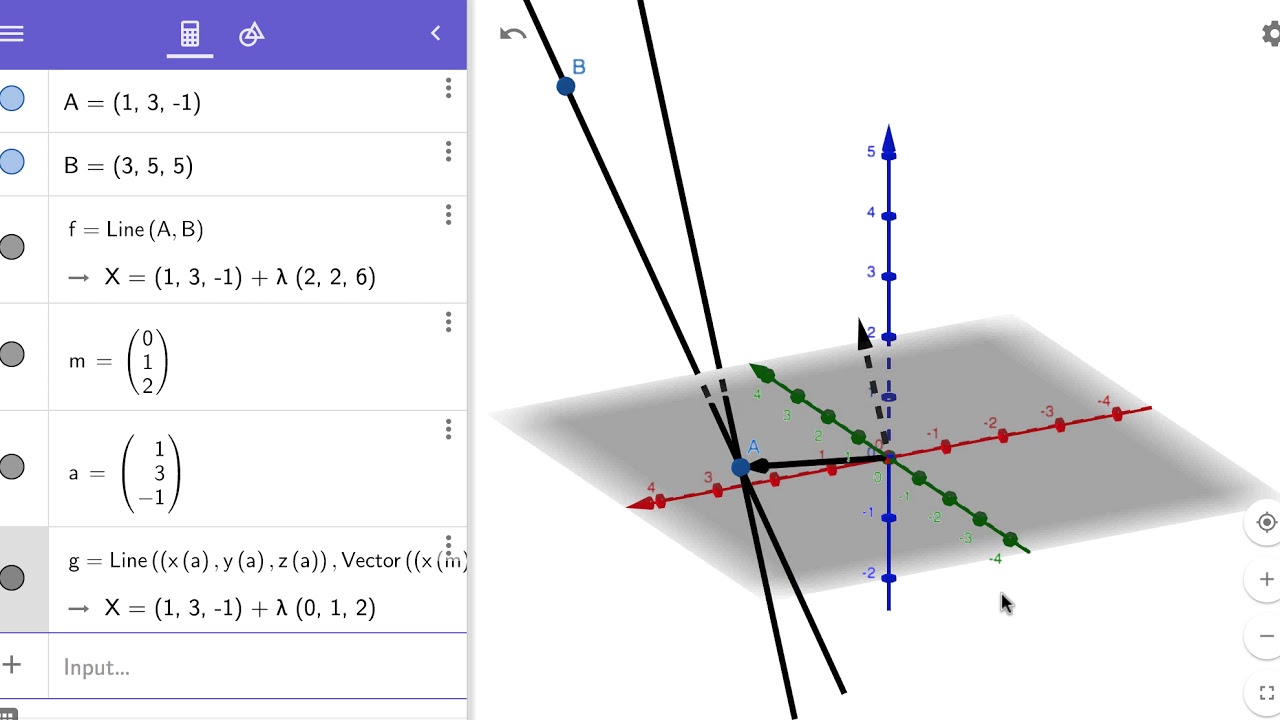
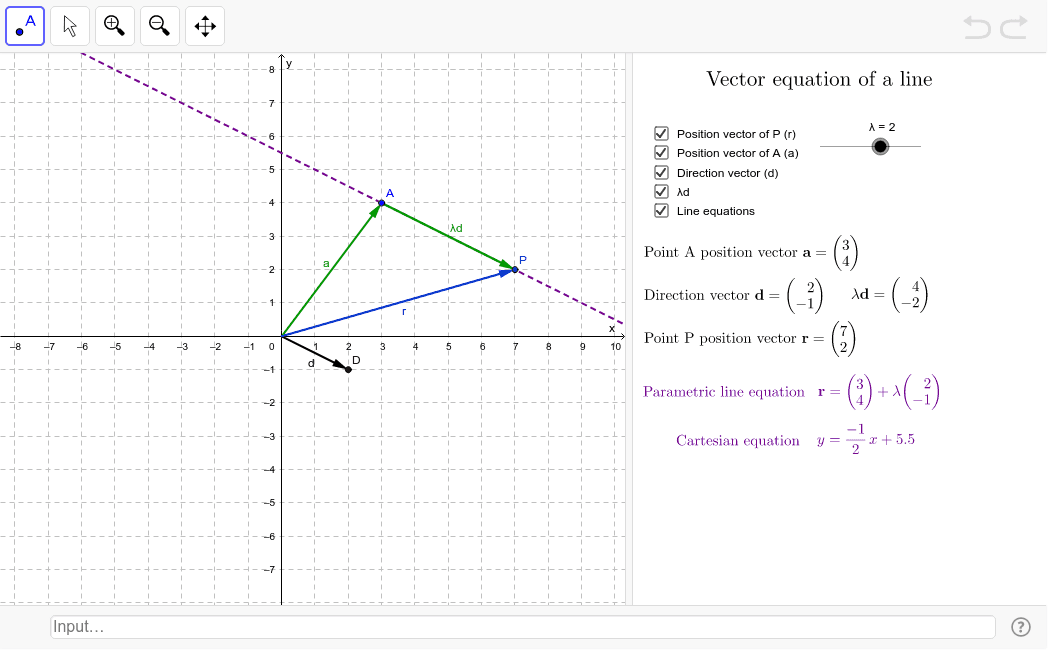
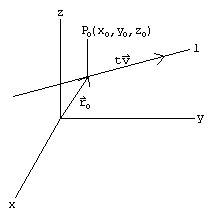
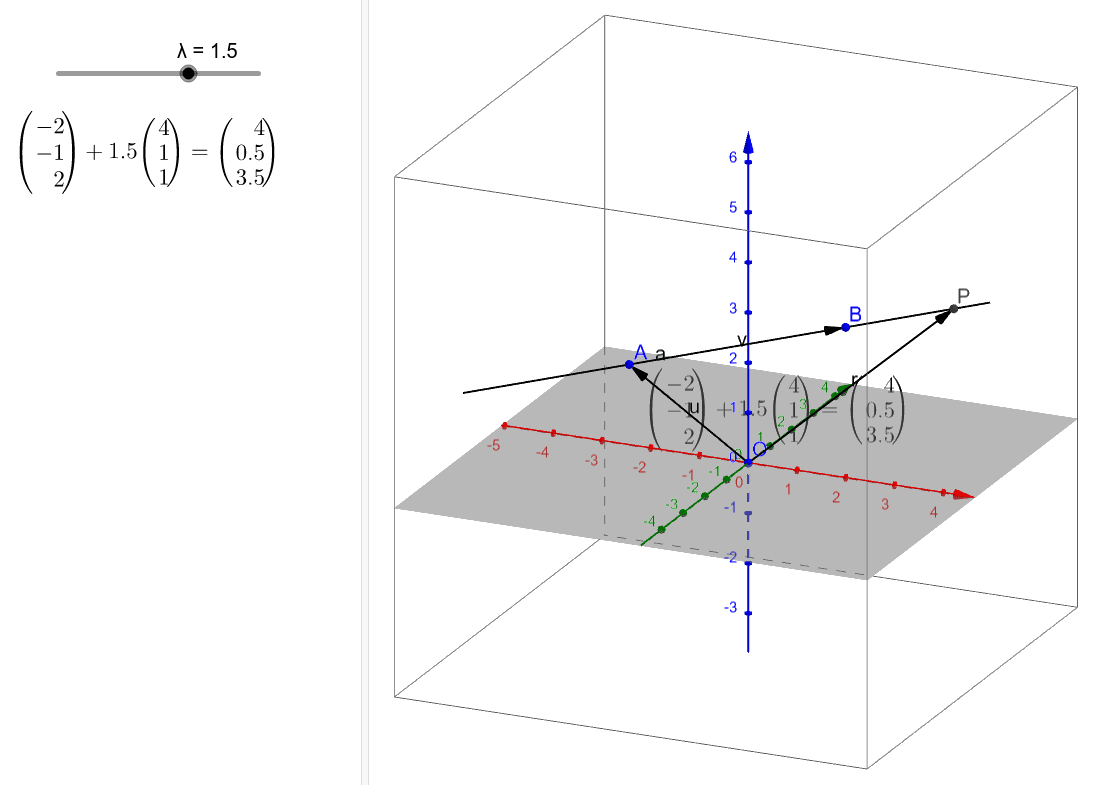
The straight line equation is found by substituting values of x 1 y 1 and m into the above. Similarly in three dimensional space we can obtain the equation of a line if we know a point that the line passes through as well as the direction vector which designates the direction of the line. So general equation of straight line is stated as the equations of both plane together ie. Features finding the equation of the line through two points in 3d space in vector form parametric form and cartesian form.

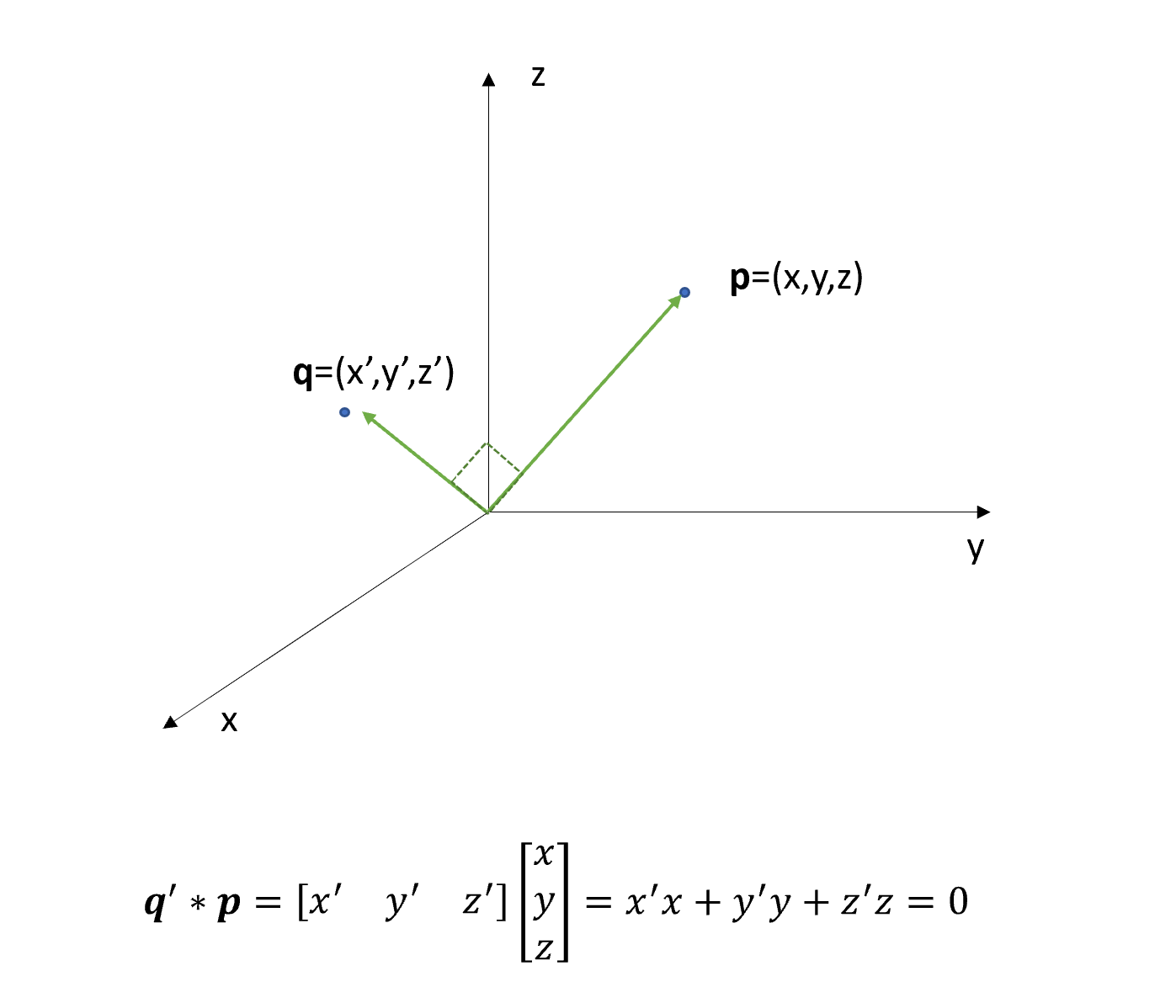
The equation of a line with direction vector vec d lmn d lmn that passes through the point. Vectors can be defined as a quantity possessing both direction and magnitude.