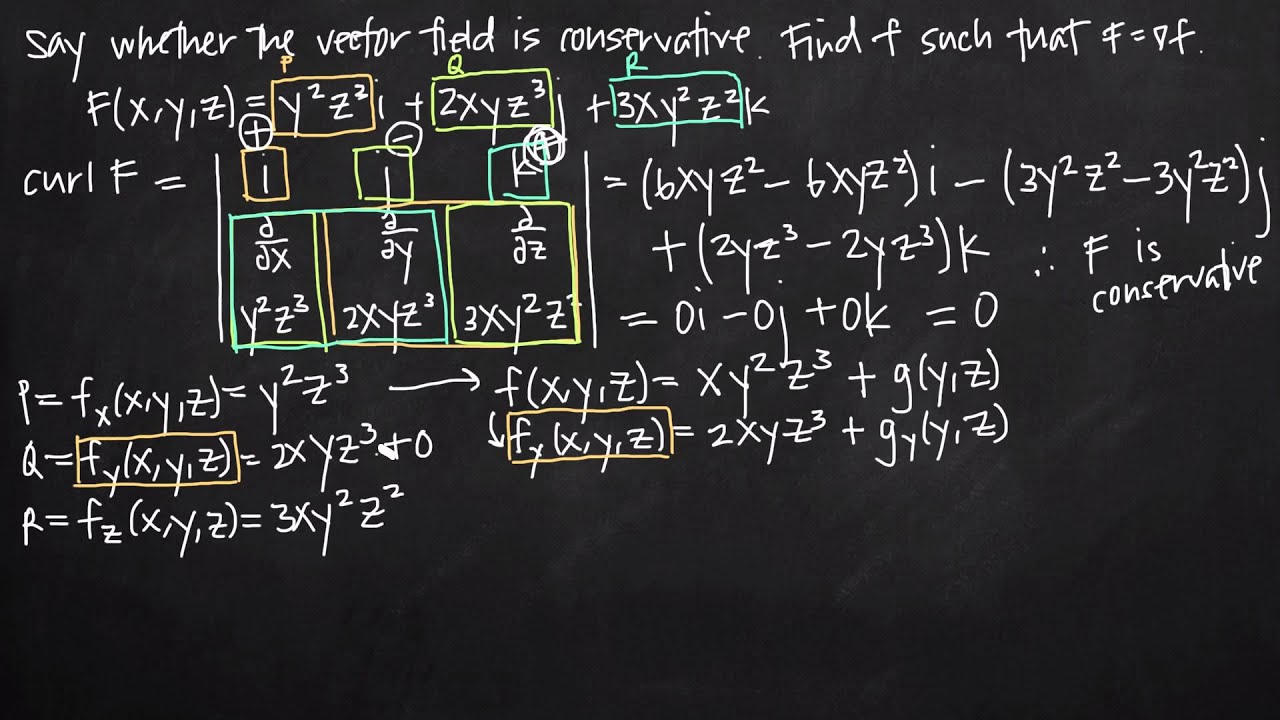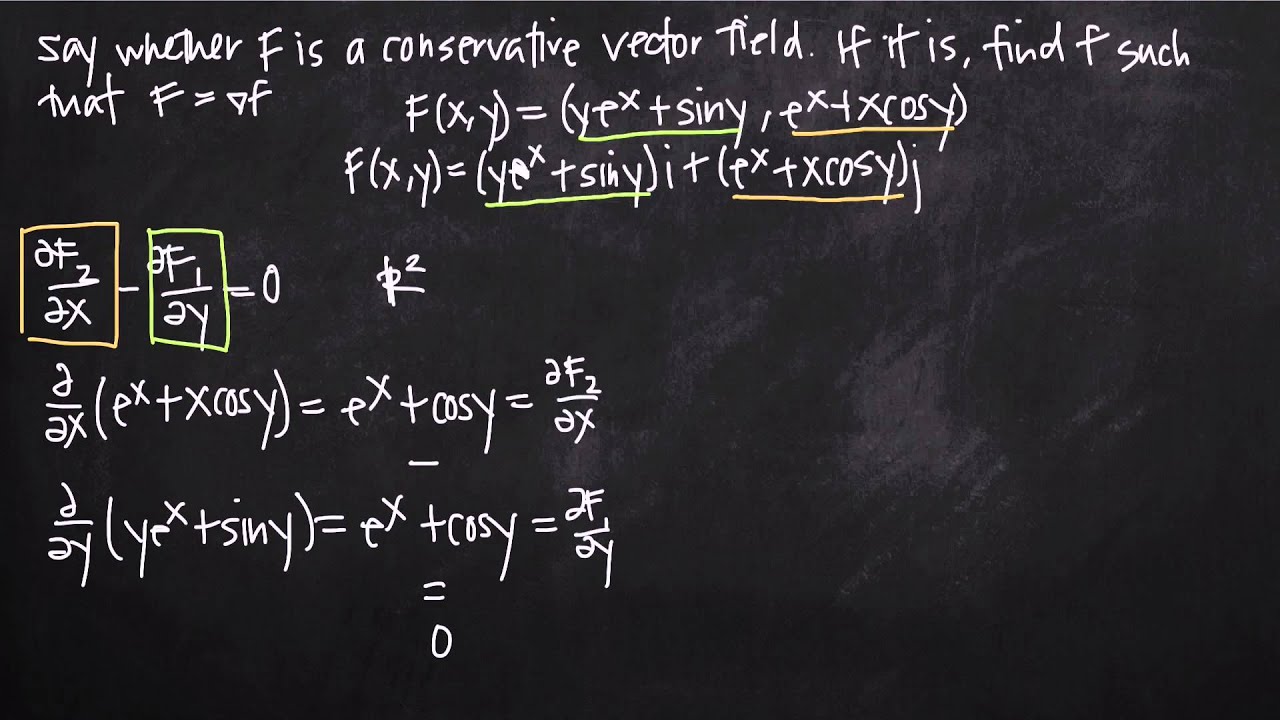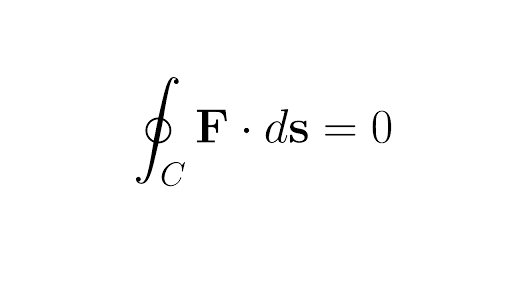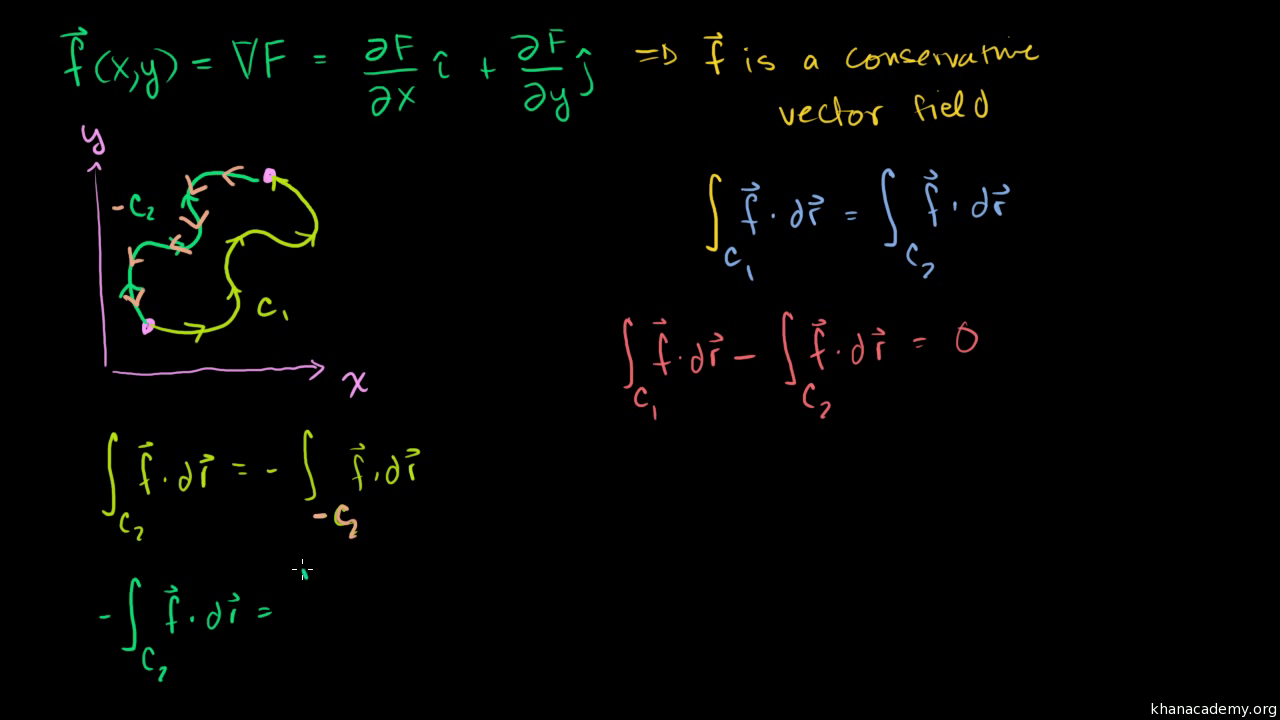How To Determine If A 3d Vector Field Is Conservative

In three dimensions this means that it has vanishing curl.

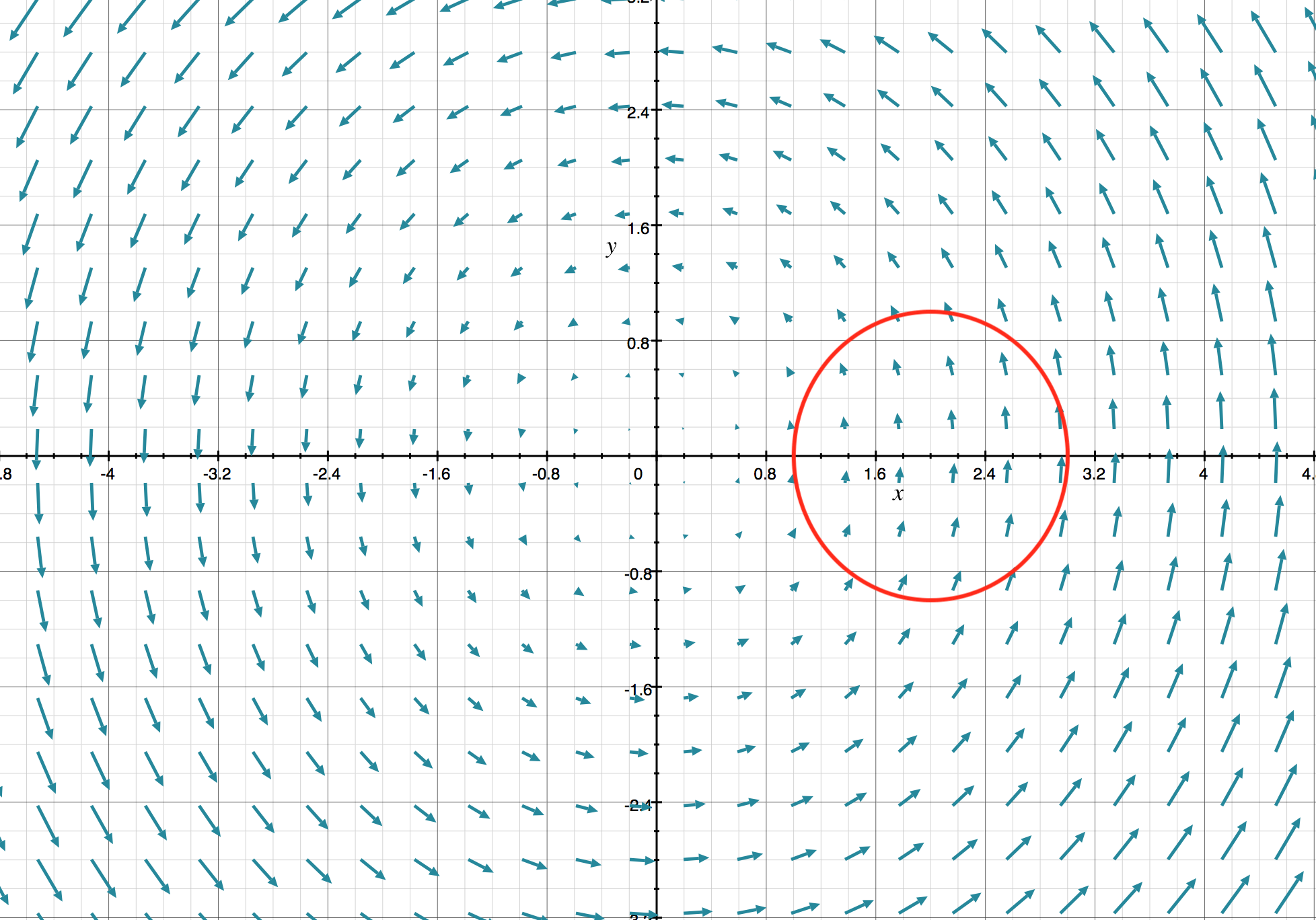
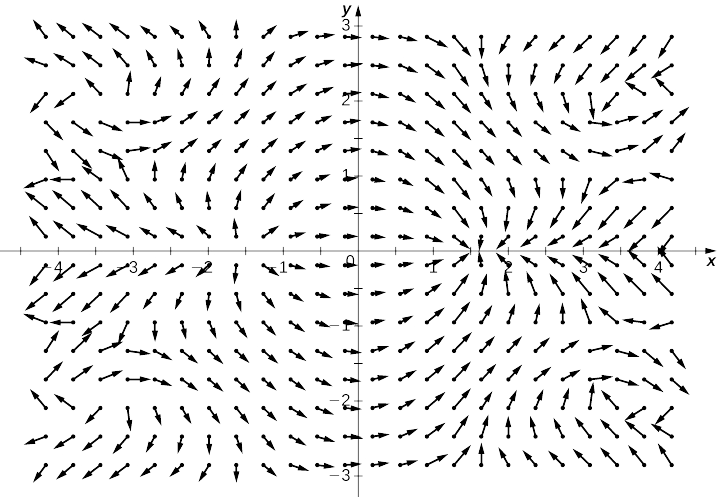
How to determine if a 3d vector field is conservative. How to determine if a vector field is conservative. In vector calculus a conservative vector field is a vector field that is the gradient of some function. A conservative vector field has no circulation. Especially important for physics conservative vector fields are ones in which integrating along two paths connecting the same two points are equal.

A conservative vector field is also irrotational. A simple example of using the gradient theorem. The choice of any path between two points does not change the value of the line integral. If vec f is a conservative vector field then the function f is called a potential function for vec f.

Conservative vector fields have the property that the line integral is path independent. However in pure math this is not always quite the case. Finding a potential function for three dimensional conservative vector fields. A vector field vec f is called a conservative vector field if there exists a function f such that vec f nabla f.

F 0 everywhere in w then f is conservative within the domain w. Most fields that you will deal with especially in physics will only need to satisfy clariauts theorem to be conservative. All this definition is saying is that a vector field is conservative if it is also a gradient vector field for some function. Now as noted above we dont have a way yet of determining if a three dimensional vector field is conservative or not.

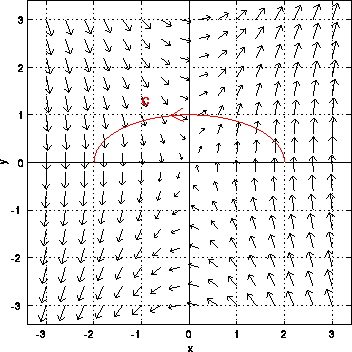
Line integrals in vector fields articles line integrals in a vector field. Google classroom facebook twitter. Conservative force in physics any force such as the gravitational force between the earth and another mass whose work is determined only by the final displacement of the object acted upon. 15 between point p 0 and point p 1 is independent of the path between these two points.

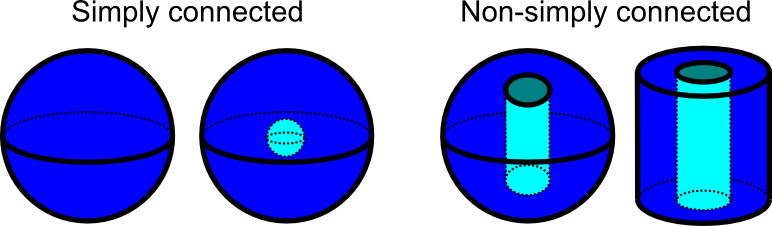
However if we are given that a three dimensional vector field is conservative finding a potential function is similar to the above process although the work will be a little more involved. Determine whether a vector field is conservative. Our vector function is continuous well behaved so this field is conservative. One subtle difference between two and three dimensions is what it means for a region to be simply connected.

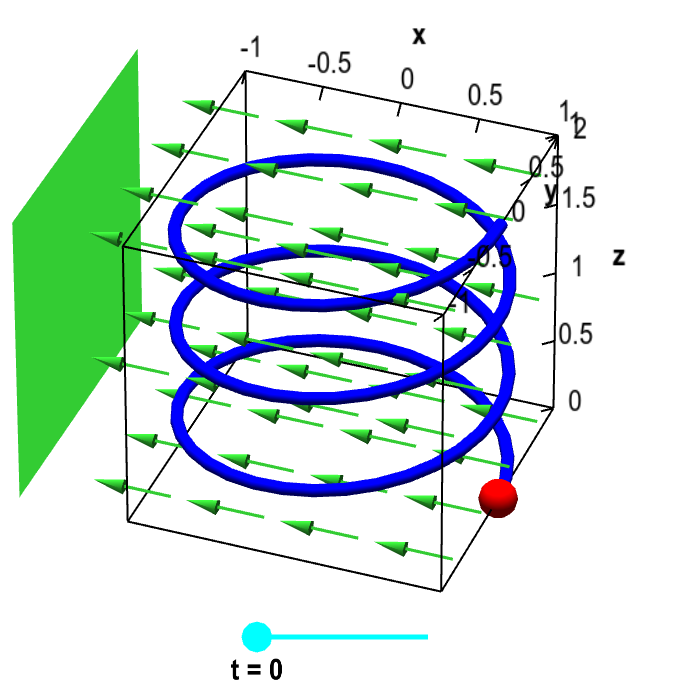
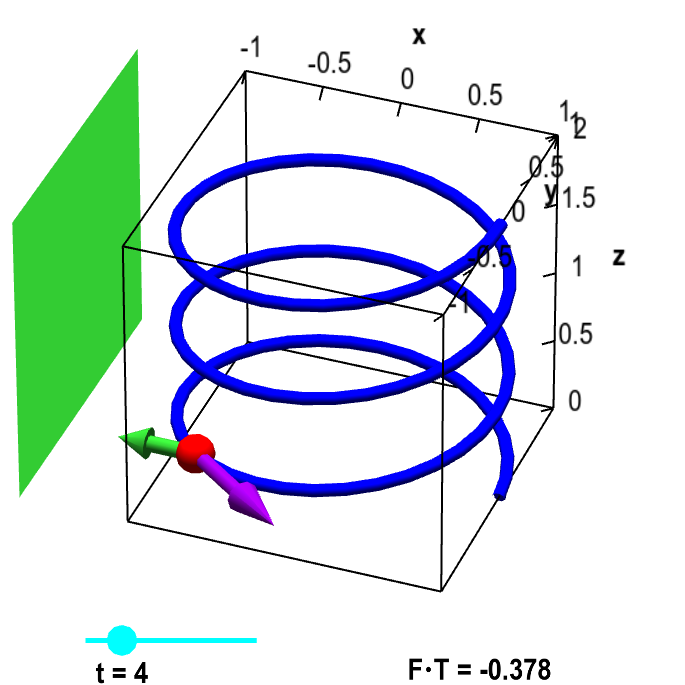
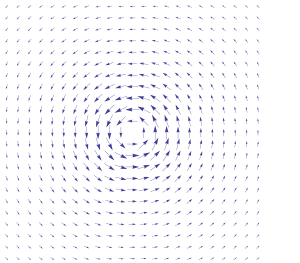
Finding a potential function for conservative vector fields. A path dependent vector field with zero curl.