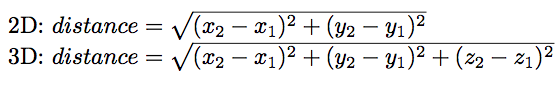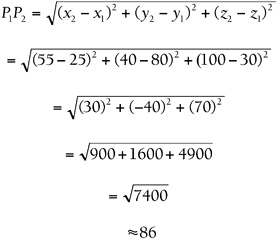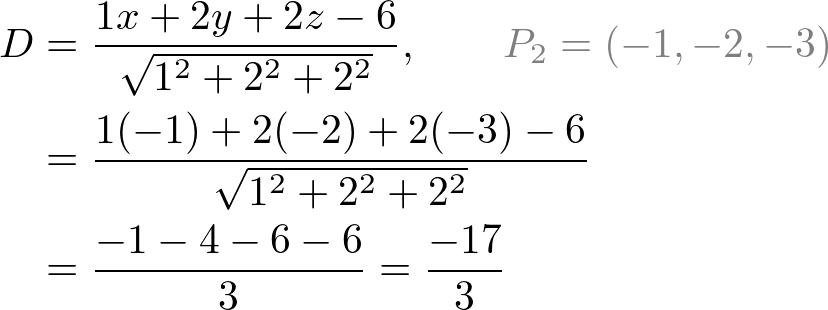Distance Formula In 3d

In both 1d and 2d the distance function satisfies the following properties.

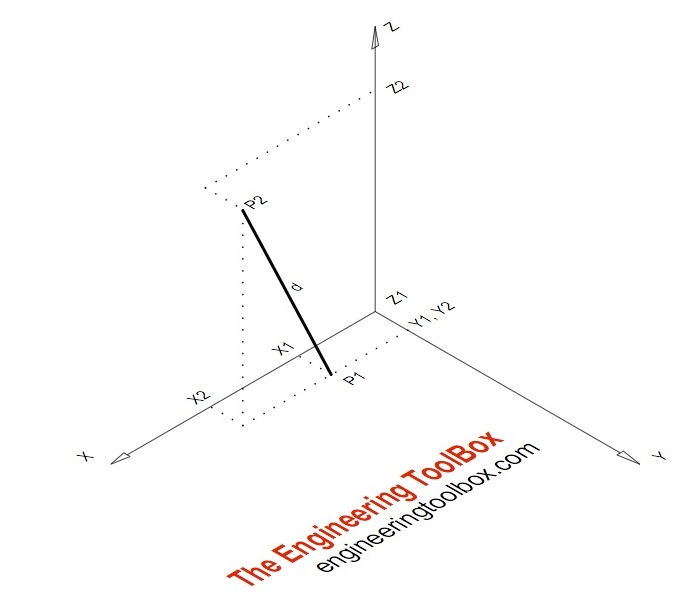
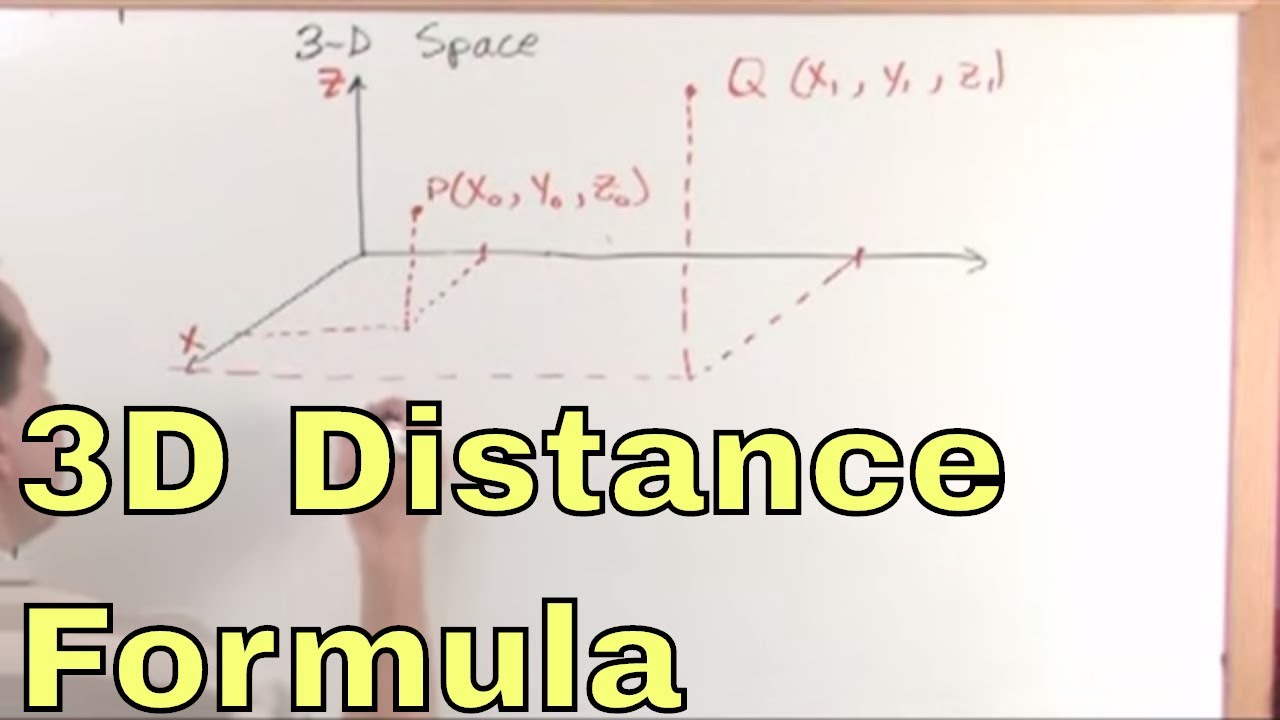
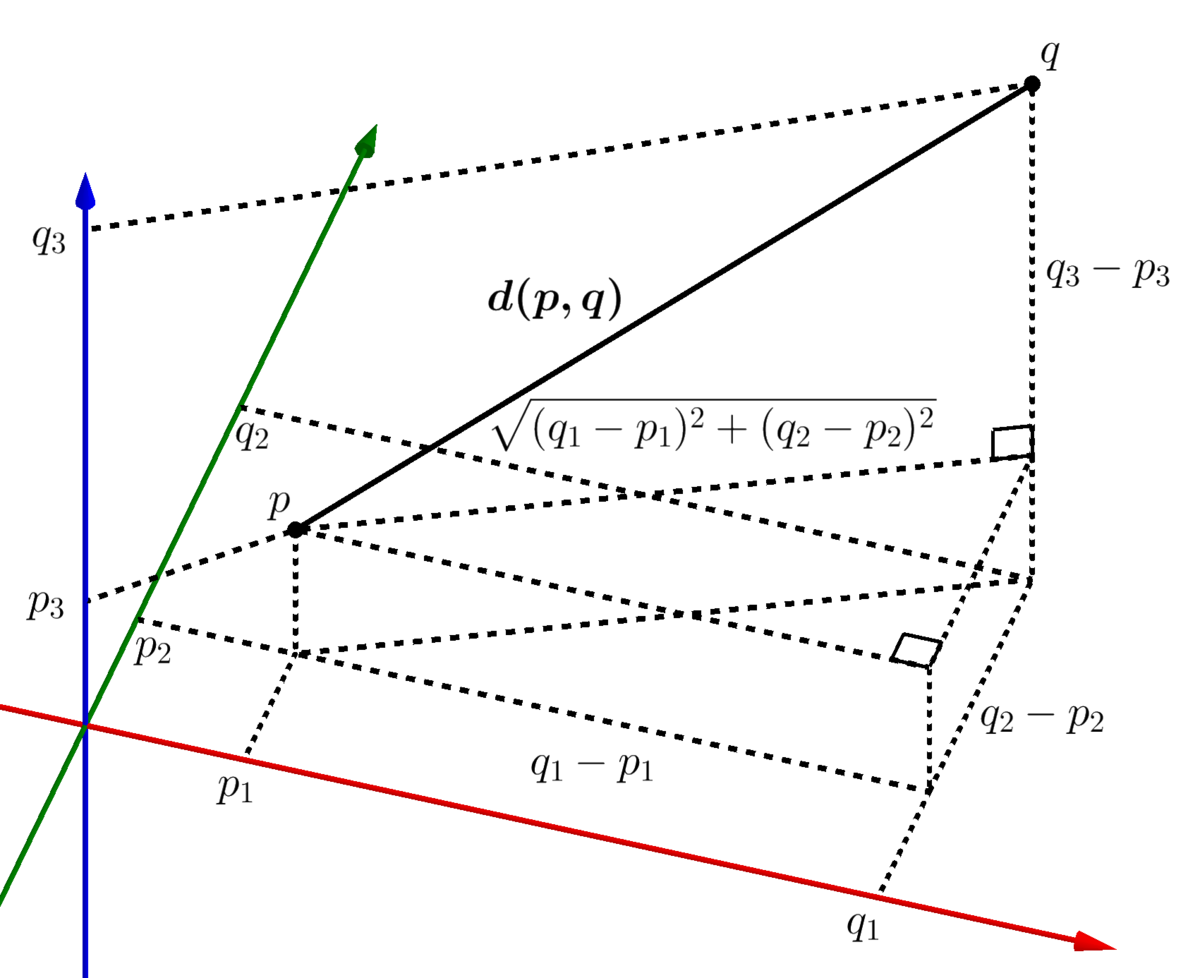
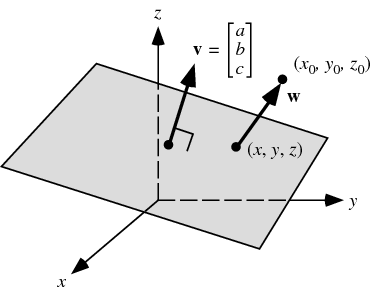
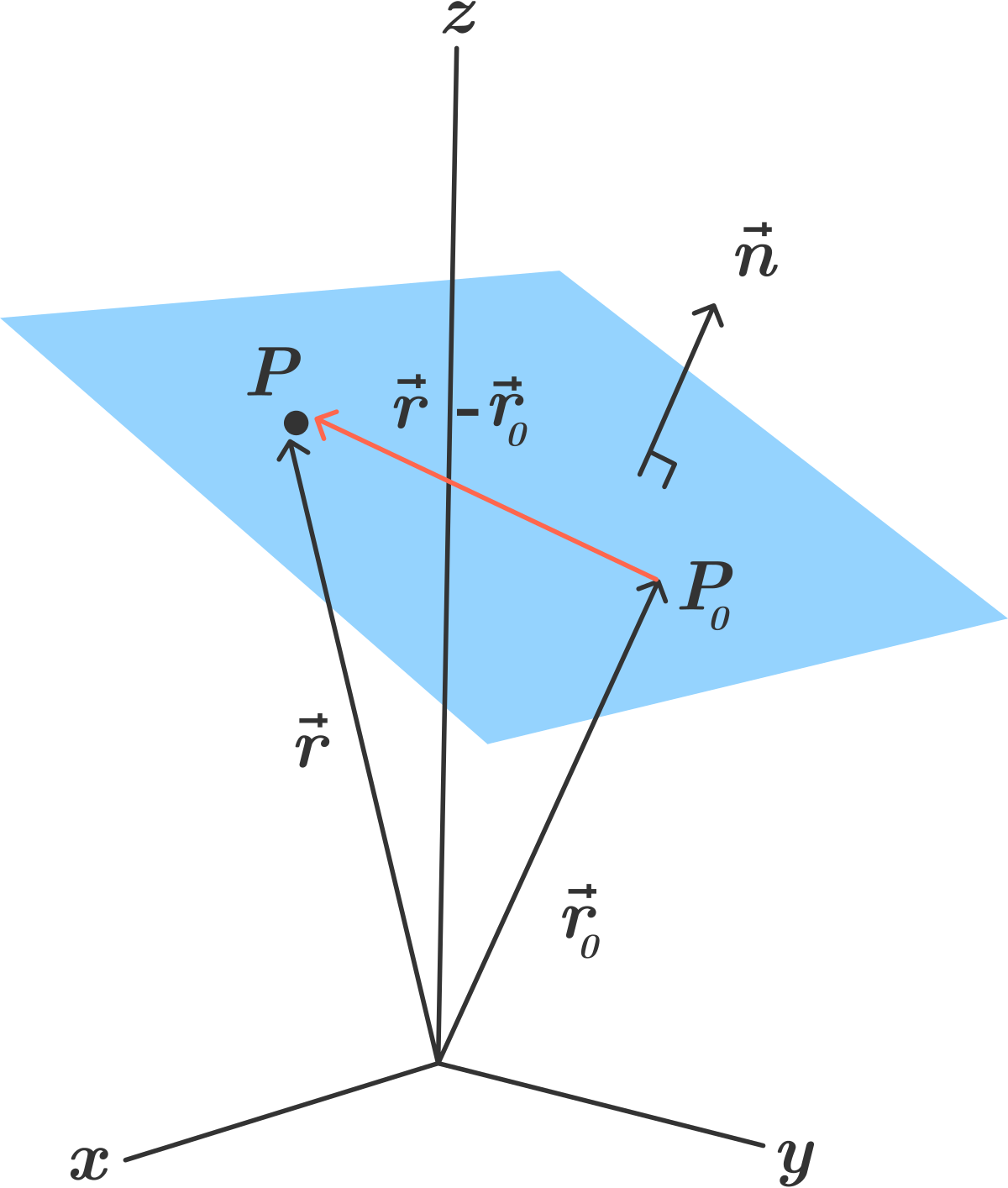
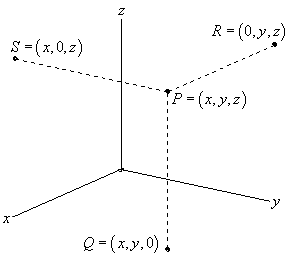
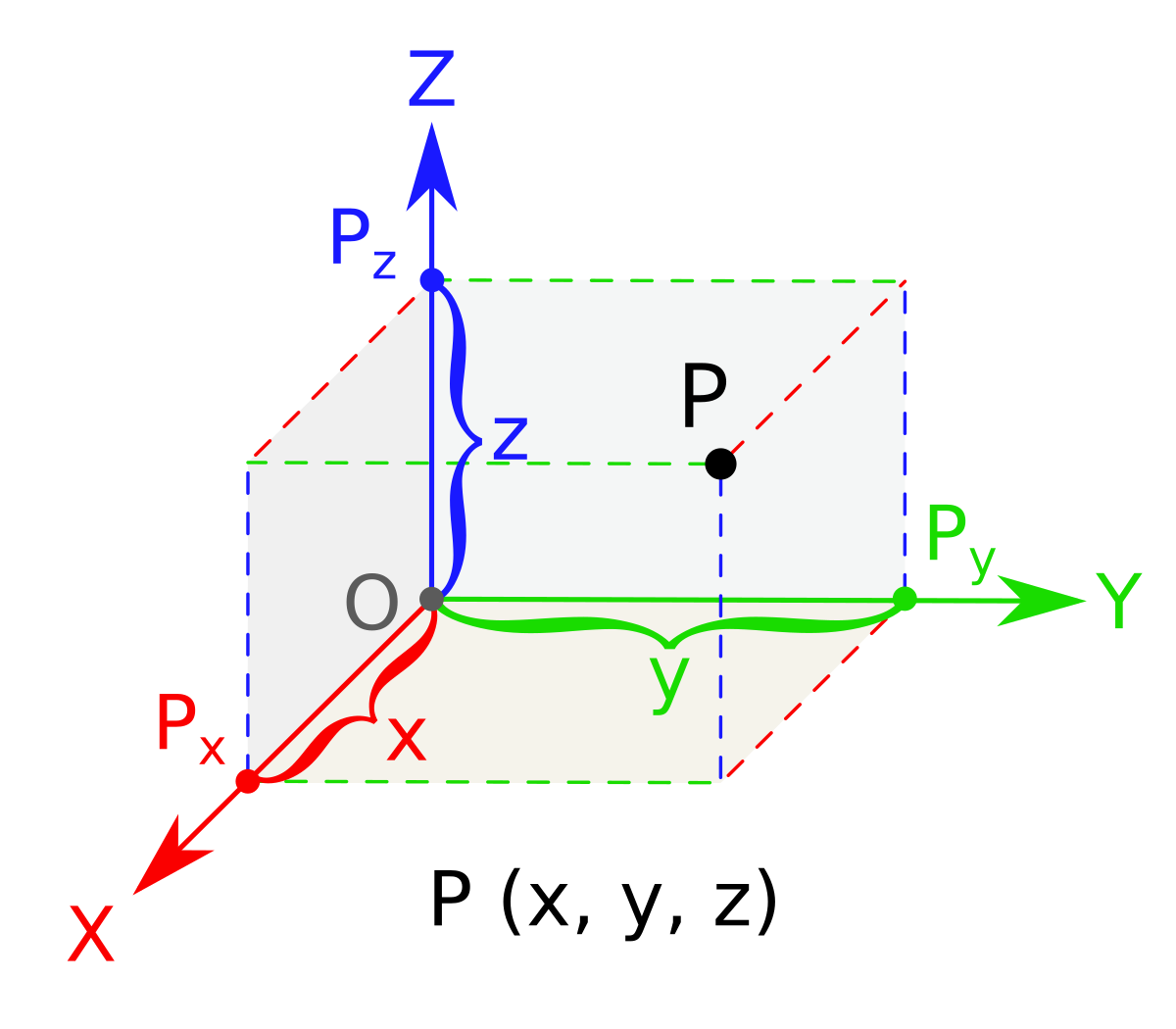
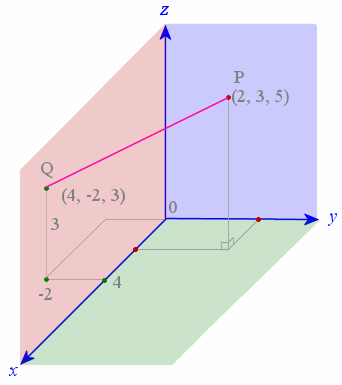
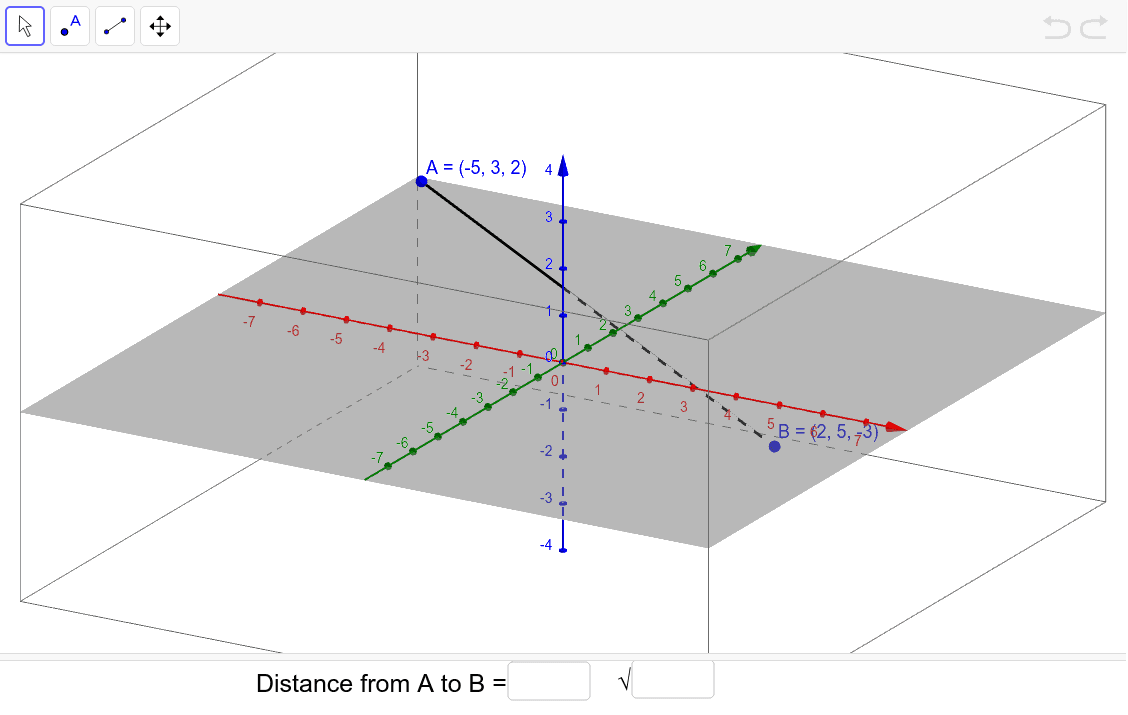
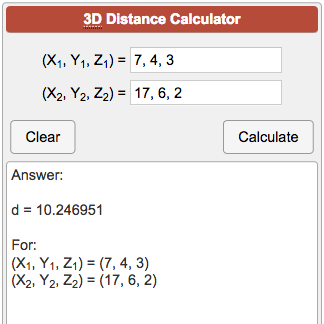
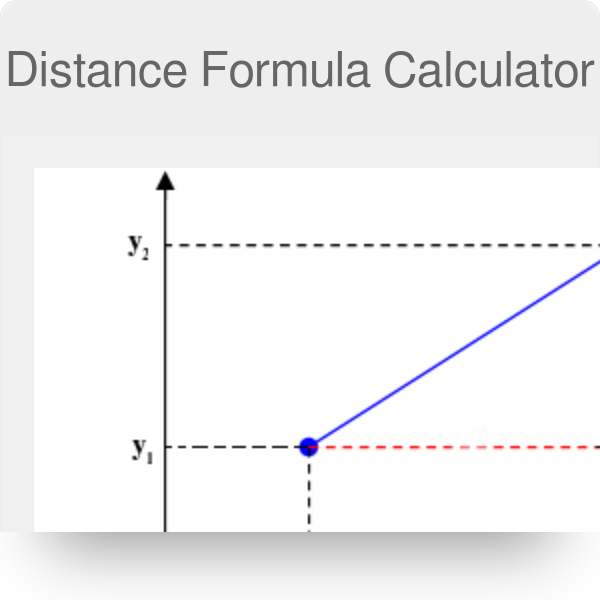
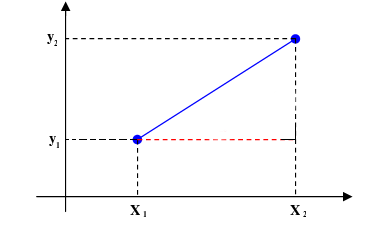
Distance formula in 3d. 1 101 text and 205. Similarly the distance between two points p 1 x 1y 1z 1 and p 2 x 2y 2z 2 in xyz space is given by the following generalization of the distance formula dp 1p 2 p x 2 x 12 y 2 y 12 z 2 z 12. Enter 2 sets of coordinates in the 3 dimensional cartesian coordinate system x 1 y 1 z 1 and x 2 y 2 z 2 to get the distance formula calculation for the 2 points and calculate distance between the 2 points. Example the distance between p 1 231 and p 2 8.

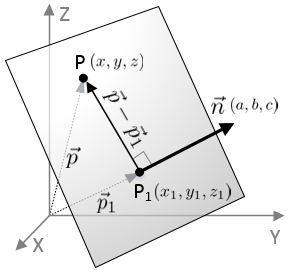
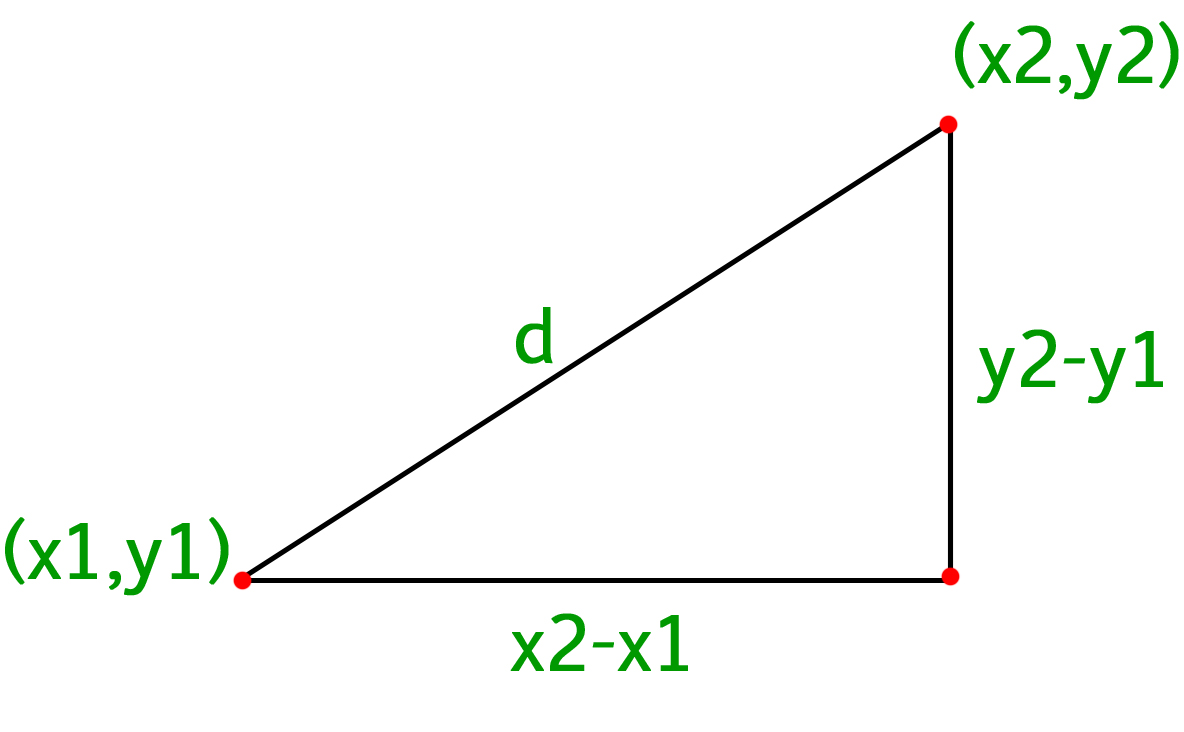
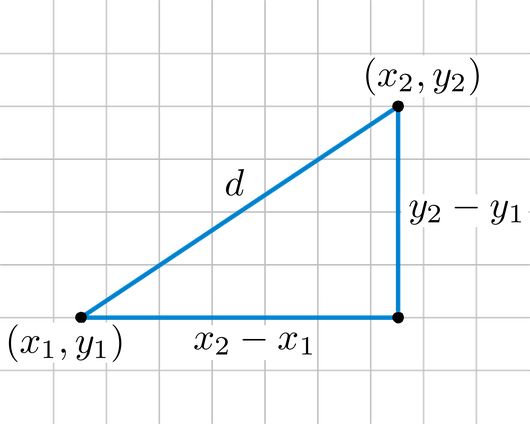
Distance formula dp 1p 2 p x 2 x 12 y 2 y 12. Thus the formula to find the distance between two points in three dimension is given by. This is a basic example of a metric space the euclidean metric and the metric is induced by a norm ell2 norm and that norm comes from an inner product so this is an example in a lot of places and i can give you references for. D p q 0d pq geq 0 dpq 0 for all pointsp qpq pq with equality if and only ifp qp q p q d p q d q pd p q d q p dpq dqp for all pointsp qpq pq d p q d p r.

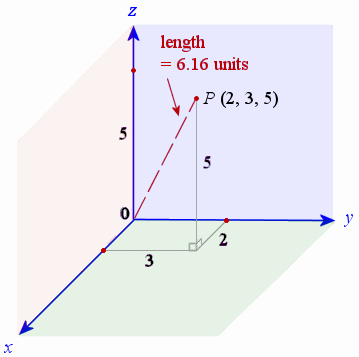
The above equation is the general form of the distance formula in 3d space. Distance below is the implementation of above formulae. A special case is when the initial point is at the origin which reduces the distance formula to the form. This can be proved by repeated application of the pythagorean theorem.

D x 2 y 2 z 2 dsqrt x 2 y 2 z 2 d x 2 y 2 z 2 where x y z xyz x y z is the terminal point. Distance formula 3d textdistance sqrtx1 x22y1 y22z1 z22 practice problems find the distance between the two points in 3d space. The formula for distance between two points in 3 dimension ie x1 y1 z1 and x2 y2 z2 has been derived from pythagorean theorem which is. A b x 2 x 1 2 y 2 y 1 2 z 2 z 1 2.